Курсовая работа: Розрахунок слідкуючої системи

j₃ = -arctg(0,008×w)

Тоді маємо j(w)=– 90°– arctg(0,4×w) – arctg(0,01×w);

По одержаним залежностям будуємо графік.

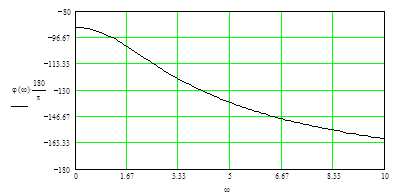
Рис. 8. ЛФЧХ розімкненої корегованої системи.

12.2 Перехідна функція замкненої корегованої системи

Передавальна функція замкненої корегованої системи має вигляд:

де G₀ = T₂ /T₁ = 0,283/0,65 = 0,435

Маємо a = 1/р тоді

Підставивши числові значення одержимо

Запишемо характеристичне рівняння системи:

0 ,00 1132 р⁴ + 0, 12 р³ + 0, 693 р² + 2 2 , 22 р + 3 2 , 62 = 0

За допомогою ЕОМ знаходимо корені рівняння (19):

р₁ = –101,9;

р₂ = –2,175 – 23,961j= 24,06·e^{85° j} ;

р₃ = –2,175 + 23,961j= 24,06·e^{-85° j} ;

р₄ = –1,746.

Далі для знаходження оригіналу h(t) скористаємося другою теоремою Хевісайда , суть якої в наступному : якщо зображення F(p)функції f(t)має вигляд

;

то її оригінал дорівнює

де p_k – корені характеристичного рівняння.

В нашому випадку F₁ (p) = 32,6·(0,65р + 1);

F₂ (p) = 0,001132р⁴ + 0,12р³ + 0,693р² + 22,22р + 32,62;

F’₂ (р) = 0,00453р³ + 0,36р² + 1,386р + 22,22.

Знайдемо значення F’₂ (р_к ) , де p_k – корені характеристичного рівняння.