Курсовая работа: Статистические распределения и их основные характеристики
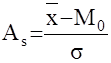
AS может быть положительным и отрицательным.
Положительная величина указывает на наличие правосторонней асимметрии
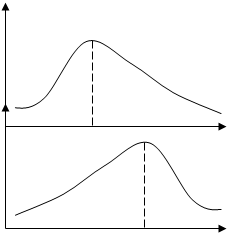 |
(
Отрицательный знак свидетельствует о наличии левосторонней асимметрии
(![]() )
)
Другим показателем асимметрии, предложенный шведским математиком Линбергом, рассчитывают по формуле:
AS = П - 50,
где П - процент тех значений признака, которые превосходят по величине среднюю арифметическую.
Наиболее точным и распространенным является показатель, основанный на определении центрального момента третьего порядка (в симметричном распределении его величина равна 0).
Моментом распределения называется средняя арифметическая тех или иных степеней отношения индивидуальных значений признака от определенной исходной величины.
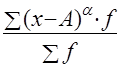 ,
,
где А - величина, от которой определяется отклонение
a - степень отклонения (порядок момента)
В зависимости от того, что принимают за величину А, различают три вида моментов:
Начальные моменты получают при А=0
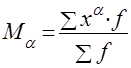
Центральные моменты получают при А=
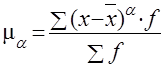
Условные моменты ma получают при А, не равной средней арифметической и отличной от нуля:
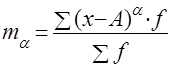
В статистической практике пользуются моментами превого, второго, третьего и четвертого порядков.
| Моменты распределения порядка | Начальные | Центральные | Условные |