Курсовая работа: Статистические распределения и их основные характеристики

Значение переменнойЧастота повтора

f

n- f

Отсюда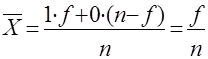

Дисперсия

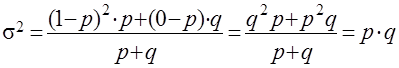
Средняя квадратичная равна

.

Например в результате контроля из 1000 готовых изделий 20 - бракованных.

Отсюда

1 - соответствует бракованным изделиям

0 - годной продукции

Процент барка равен .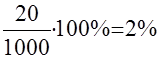

Тогда величина дисперсии

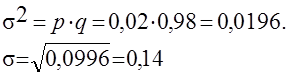
Если признак принимает больше двух значений, то оценка вариации равна

,

где W- доля каждого признака.

Для получения приблизительного представления о форме распределения строят графики распределения (полигон и гистограмму). Число наблюдений, по которому строится эмпирическое распределение, обычно невелико. С увеличением числа наблюдений и одновременным уменьшением величины интервала зигзаги полигона начинают сглаживаться и в результате чего получается плавная кривая, которая называется кривой распределения.

Если кривая построена по данным наблюдения, то она называется эмпирической кривой, а если она отражает закономерность соотношения вариант и частот, то она называется теоретической кривой. Исследование закономерности (формы) распределения включает решение трёх последовательных задач:

выяснение общего характера распределения

выравнивание эмпирического распределения, которое состоит в том, что на основании эмпирического распределения строится кривая y=f (x)

проверка соответствия найденного теоретического распределения эмпирическому.

В практике статистического исследования встречаются различные распределения.

Однородные совокупности характеризуются, как правило, одновершинными распределениями. Многовершинность свидетельствует о неоднородности. Появление двух вершинной или асимметричной кривой означает, нарушение при изменении условий получения и обработки сведений в этом случае необходима перегруппировка данных.

Выявление общего характера распределения предполагает не только степень его однородности, а также вычисление показателей асимметрии и эксцесса.

Симметричным является распределение в котором частота любых двух вариантов равноотстоящих в обе стороны от центра распределения, равны между собой. Для симметричного распределения

.

Поэтому показатель асимметрии, основан на соотношении показателей центра распределения: чем больше разница между средними () тем больше асимметрия ряда.