Математика / Курсовая работа: Строение конечной группы 24-го порядка, заданной образующими и определяющими соотношениями G

Курсовая работа: Строение конечной группы 24-го порядка, заданной образующими и определяющими соотношениями G

L1={e,a1,c1,c4,c5,c6,c7,f1,h5,h10,l1,l2} Z12

При нахождении подгрупп удобно будет пользоваться следующими

соображениями:

1. В нашем случае, согласно теореме Лагранжа, возможны подгруппы порядков 2, 4, 6, 8, 12 и тривиальные – 1, 24. Поэтому, необязательно для получения подгруппы G искать все 24 элементов, нужно найти всего 13 элементов.

2. Если на каком-то шаге мы нашли, что в нашей подгруппе имеются элементы x и y, то подгруппа тривиальная. Ведь {x,y} – это минимальная система образующих нашей группы.

e a1 c1,c6 c4,c5 c3,c8 C2,h11 C7,h10 H1,h6 H2,h7 H3,h4 H8,h9 F1,h5 L1,l2
a1 A1 C1 F1 H1 H3 L1 H3 H1 H2 H2 F1 L1
c1,c6 C1 L1 H1 H3 L1 H3 H1 H2 H2 L1 L1
c4,c5 F1 G G L1 G G G G F1 L1
c3,c8 H1 G G G H1 G G G G
C2,h11 H3 G H3 G G G G G
C7,h10 L1 G G G G L1 L1
H1,h6 H3 G G G G G
H2,h7 H1 G G G G
H3,h4 H2 H2 G G
H8,h9 H2 G G
F1,h5 L1 L1
L1,l2 L1

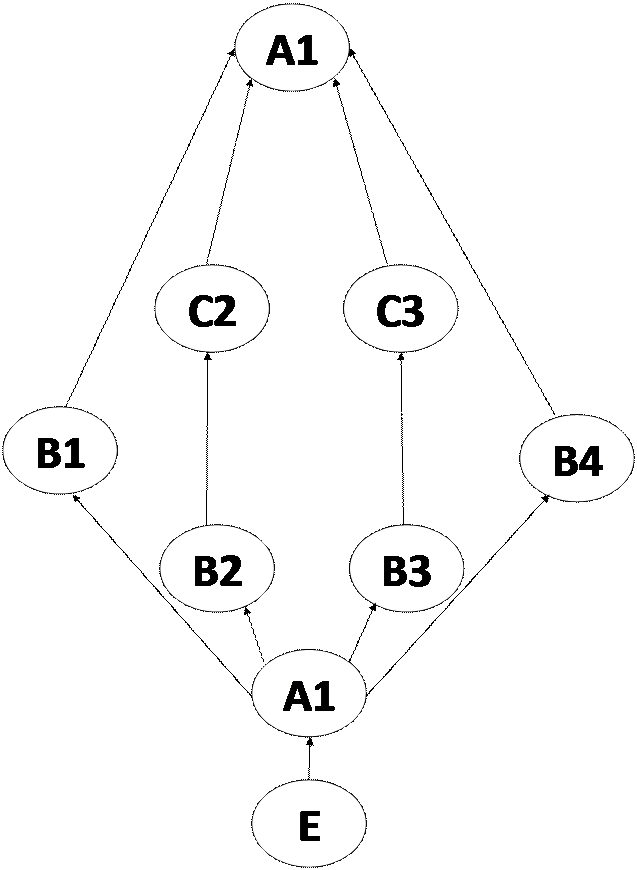
2. 5 Структура всех подгрупп.

1. А.В. Клюшин «Введение в дискретную математику» МИЭТ, 2004г.

2. А.В. Клюшин «Курс лекций по дискретной математике 2009-2010 уч. год.»

3. Кострикин А.И. «Введение в алгебру», т.1, 3.

К-во Просмотров: 362
Бесплатно скачать Курсовая работа: Строение конечной группы 24-го порядка, заданной образующими и определяющими соотношениями G