Курсовая работа: Строение конечной группы 24-го порядка, заданной образующими и определяющими соотношениями G

сокращать и записывать как z n+m . Например, х 3 х -4 = х -1 , х 2 х -2 = е .

На множестве слов рассмотрим бинарную операцию (·) , которую будем на-

зывать умножением. Если u=z 1 ...z n и v = t 1 …t m - два слова, то их произведением

будем называть слово uv = z 1 ...z n t 1 ...t m , в котором произведены все возможные

сокращения. Если одно из слов равно е , то положим е·u = u·е = u . Несложно

видеть, что данная бинарная операция ассоциативна, а элемент е является

единицей. Кроме того, каждое слово имеет обратное. Действительно, если u =

z 1 ...z n , то u -1 = 1 1

n 1 z - ...z - .

Таким образом, множество всех слов в данном алфавите с определенной

выше бинарной операцией будет группой. Эта группа называется свободной

группой с двумя образующими х, у .

Аналогично можно определить свободную группу с тремя образующими и

т.д.

Пусть F - свободная группа с образующими x 1 ...x n . Равенство двух слов u=v

будем называть соотношением. Всякое соотношение можно записать в виде u·v -1 =

е . Пусть задана система из k соотношений

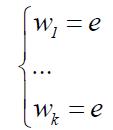(1)

Рассмотрим все нормальные подгруппы группы F , содержащие слова w 1 ,...,

w k Одной из таких подгрупп является сама группа F. Пересечение всех нормальных

подгрупп, содержащих w 1 ,..., w k , обозначим N . Можно показать, что пересечение

нормальных подгрупп всегда будет являться нормальной подгруппой. Таким

образом, N будет наименьшей нормальной подгруппой, содержащей элементы

w 1 ,..., w k . Пусть G = F/N - фактор-группа. Напомним, что элементами фактор-

группы являются смежные классы по подгруппе N . Если u - слово, u Î F, то через

u будем обозначать смежный класс, содержащий u . Тогда в фактор-группе G

справедливы равенства 1 w = k w = 1 . Группу G будем называть группой с

образующими x 1 ...x n и соотношениями (1) и задавать в следующем виде

1 n 1 1 k k G=<x ,...,x | u = v ,...,u = v >