Курсовая работа: Теория эллиптических интегралов и эллиптических функций

Установим две формулы для эллиптической функции, из которых одна будет давать ее разложение на сумму простейших элементов с явным выделением ее полюсов и их главных частей, а другая будет представлять эллиптическую функцию посредством отношения произведений элементарных множителей с явным выделением ее нулей и полюсов. Прежде чем приступить к осуществлению этой задачи, мы установим ряд общих свойств эллиптической функции.

Примечание - при определении эллиптической функции предполагалось, что отношение

ее первоначальных периодов является мнимым числом. Если это отношение есть число действительное, то функция является просто периодической или приводится к постоянному. Кроме того, во всем дальнейшем будем считать коэффициент при мнимой части отношения положительным, так как это достижимо путем изменения знака у одного из первоначальных периодов.

1.2 Параллелограммы периодов

Чтобы дать геометрическое истолкование двоякой периодичности, рассмотрим в плоскости комплексного переменного четыре точки

считая произвольным комплексным числом.

Так как отношение есть мнимое число, то эти четыре точки изображают вершины некоторого параллелограмма P .

Полагая

,

мы видим, что четыре точки, упомянутые выше, есть вершины параллелограмма , который может быть получен из основного параллелограмма посредством некоторого сдвига.

Придавая m и n всевозможные целые значения, мы получим сеть параллелограммов , конгруэнтных между собой и покрывающих всю плоскость (рис. 1).

Чтобы любые два параллелограмма нашей сети не имели общих точек, условимся причислять к каждому параллелограмму лишь часть его границы, а именно стороны

,

,

за исключением концов

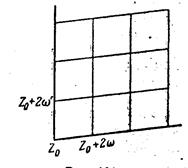
Рисунок 1 – Сеть параллелограммов

Что же касается двух сторон параллелограмма , мы их будем рассматривать принадлежащими к смежным параллелограммам с . Тогда любая точка плоскости принадлежит одному и только одному из этих параллелограммов, например .

Точки вида

,

где и - любые целые числа, называются конгруэнтными или эквивалентными с точкой z ; в параллелограммах они занимают то же положение, что и точка z в .

Среди этих эквивалентных точек имеется одна точка, которая принадлежит основному параллелограмму P (эта точка .

Итак, можно сказать, что всякая точка плоскости эквивалентна некоторой и притом единственной точке основного параллелограмма Р . Будем называть параллелограммы параллелограммами периодов; выбор среди них основного параллелограмма Р , очевидно, произволен. Теперь можно геометрически истолковать соотношение (2). Они выражают, что функция f ( z ) принимает одно и то же значение во всех эквивалентных точках. Следовательно, достаточно изучить эллиптическую функцию в одном из параллелограммов, чтобы знать ее поведение во всей плоскости.

1.3 Основные теоремы

Теорема 1. Производная эллиптической функции есть также функция эллиптическая. В самом деле, дифференцируя соотношение (1), имеющее место при любом z , получаем