Курсовая работа: Теория эллиптических интегралов и эллиптических функций

Рисунок 2

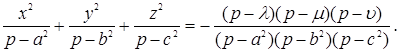
Чтобы получить (18), остается умножить обе части, соответственно, на , , и положить

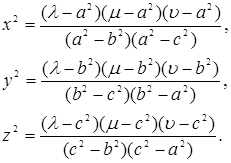(18)

Заключение

Мы дали аналитическое представление для любой эллиптической функции, отталкиваясь от сформулированного ее дескриптивного определения. Для рациональных функций мы имеем два аналитических представления. В основе перового из них лежит задание полюсов рациональной функции и соответствующих им главных частей, что приводит нас к разложению рациональной функции на простейшие дроби. В основе второго аналитического представления рациональной функции лежит задание ее нулей и полюсов, что дает нам возможность представить ее в виде отношения произведений линейных множителей.

Библиографический список

1. Лаврентьев М.А Методы теории функций комплексного переменного/ М.А.

Лаврентьев, Б.В. Шабат. – М.: Лань, 2002 – 688 с.

2. Лунц Г.Л. Функции комплексного переменного с элементами операционного

исчисления/ Г.Л. Лунц, Л.Э. Эльсгольц. – М.: Лань, 2002 – 304 с.

3. Маркушевич А.А. Введение в теорию аналитических функций/ А.И

Маркушевич, А.А. Маркушевич. – М.: Просвещение, 1977 – 320 с.

4. Привалов И.И. Введение в ТФКП/ И.И. Привалов – М.: Высш. шк., 1999 –

432 с.

5. Эйдман В.Я. Основы теории функций комплексного переменного и

операционного исчисления/ В.Я. Эйдман. – М.: Физмат, 2002 – 256 с.