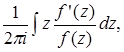Курсовая работа: Теория эллиптических интегралов и эллиптических функций

или ее полюсов мы каждый нуль или полюс считаем столько раз, какова его кратность. Для доказательства нашего утверждения прежде всего заметим, что если на границе параллелограмма периодов имеются нули или полюсы функции

f ( z ) - ,

то мы можем немного сдвинуть этот параллелограмм так, чтобы все нули и полюсы, расположенные на первоначальном параллелограмме периодов, оказались бы внутри сдвинутого параллелограмма.

Обозначим вершины этого параллелограмма через

на его сторонах нет нулей и полюсов функции

f ( z ) - .

Образуем вспомогательную функцию

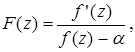
которая будет эллиптической с периодами 2 и 2, причем на сторонах рассматриваемого параллелограмма периодов она не будет иметь полюсов.

Применяя к этой функции предыдущую теорему 3, мы имеем:

(4)

где интегрирование распространено в положительном направлении по контуру упомянутого параллелограмма. С другой стороны, как известно, интеграл

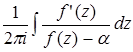
изображает разность между числом нулей и полюсов функции

f ( z ) - ,

лежащих внутри контура интегрирования.

Так как согласно формуле (4) этот интеграл равен нулю, то, следовательно, число корней уравнения

лежащих внутри параллелограмма периодов, совпадает с числом полюсов функции f ( z ) , расположенных внутри того же параллелограмма. Таким образом, теорема доказана.

Если f ( z ) принимает в параллелограмме периодов всякое значение s раз, то она называется эллиптической функцией порядка s.

В силу теоремы 3 не может существовать эллиптической функции, имеющей в параллелограмме периодов один простой полюс. Таким образом, s всегда не меньше двух, т. е. не существует эллиптических функций первого порядка. В дальнейшем мы фактически построим эллиптические функции второго порядка. Существуют, конечно, и эллиптические функции более высокого порядка.

Теорема 5 . Разность между суммой всех нулей и суммой всех полюсов эллиптической функции, расположенных в параллелограмме периодов, равна некоторому ее периоду, т. е.

,

где - нули, а - полюсы, расположенные в параллелограмме периодов. Само собой понятно, что при образовании суммы нулей или суммы полюсов

каждый нуль или полюс нужно повторить слагаемым столько раз, какова его кратность. Для доказательства прежде всего заметим, что если на границе параллелограмма периодов имеются нули или полюсы эллиптической функции, то путем небольшого сдвига этого параллелограмма мы можем достигнуть того, чтобы все нули и полюсы, расположенные на первоначальном параллелограмме периодов, попали бы внутрь сдвинутого параллелограмма. Обозначим через

вершины этого параллелограмма. На его сторонах нет нулей и полюсов функции f (z) . Тогда, как известно, искомая разность между суммами всех нулей и полюсов, расположенных внутри упомянутого параллелограмма, изображается в виде интеграла