Курсовая работа: Теория эллиптических интегралов и эллиптических функций

Вообще же интеграл (13) не выражается в элементарных функциях. Можно показать, что с помощью элементарных подстановок и преобразований эллиптический интеграл преобразуется к одной из трех канонических форм

(14)

где k и l – постоянные. Интегралы (14) называют эллиптическими интегралами в форме Лежандра, соответственно, первого, второго и третьего рода. Число k называют модулем интеграла.

Подстановка

приводит интегралы (14) к тригонометрической форме

(15)

Аргумент называется амплитудой эллиптического интеграла. Для интегралов в форме (15) приняты следующие обозначения:

Особенно часто встречаются интегралы с амплитудой , равной ; они называются полными и для первых двух из них приняты специальные обозначения

Вычисление дуги эллипса

приводит к эллиптическим интегралам. Действительно, отрезок дуги, соответствующий изменению абсциссы от 0 до x равен

Где

Это – эллиптический интеграл второго рода в форме Лежандра. Полная длина эллипса выражается через эллиптический интеграл

(16)

Этому обстоятельству и обязаны своим названием эллиптические интегралы, а также их обращения – эллиптические функции.

2.2 Эллиптические координаты

Эллиптические координаты также связаны с эллиптическим функциями. Чтобы ввести их, рассмотрим уравнение

(17)

оно третьей степени по p имеет при фиксированных x , y , z три действительных корня , , , удовлетворяющих неравенству

.

Эти корни называются эллиптическими координатами точки (x , y , z ). Система координат (,, ) ортогональна, так как поверхности

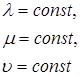
представляют собой, соответственно, софокусный эллипсоид, однополосный и двуполосный гиперболоиды, т.е. взаимно ортогональные поверхности (рис. 2).

Нетрудно вывести формулы, выражающие декартовы координаты через эллиптические. Для этого достаточно привести левую часть (17) к общему знаменателю и, заметив, что в числителе при этом получится многочлен третьей степени относительно p со старшим коэффициентом -1, разложить его на линейные множители