Курсовая работа: Теория эллиптических интегралов и эллиптических функций

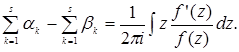(5)

При интегрировании вдоль периметра параллелограмма сумма

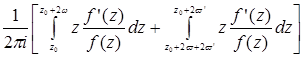
приводится посредством перемены во втором интеграле z на и

использования периодичности к следующему выражению

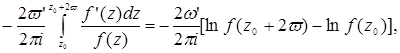
так как

,

то число в скобке есть нуль или вида

где - целое. Таким образом, сумма двух рассматриваемых интегралов вообще равна Аналогично сумма двух остальных интегралов

приводится посредством того же рассуждения к Возвращаясь к формуле (5), перепишем ее в виде

что и требовалось доказать.

Примечание - применяя доказанную теорему к функции

f ( z ) - ,

где - произвольное комплексное число, мы видим, что сумма корней уравнения

расположенных в параллелограмме периодов, конгруэнтна с суммой полюсов функции f ( z ) , лежащих в этом параллелограмме, относительно ее первоначальных периодов 2 и 2.

1.4 Эллиптические функции второго порядка

1. Если эллиптическая функция f ( z ) с периодами 2 и 2 удовлетворяет соотношению

(6)

где К - некоторое постоянное, то числа

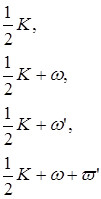
будут нули или полюсы функции f ( z ) . В самом деле, полагая в соотношении (6)

получим:

,