Курсовая работа: Теория эллиптических интегралов и эллиптических функций

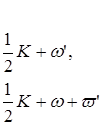
есть нули или полюсы функции f ( z ) . Числа , ', + ' и им конгруэнтные называются полупериодами.

Предполагая К = 0, т. е. что f ( z ) удовлетворяет соотношению

мы будем иметь нечетную эллиптическую функцию.

В силу доказанного для такой функции точки z равной нулю, а следовательно, все периоды, равно, как все полупериоды, будут нулями или полюсами.

2. Если эллиптическая функция f ( z ) с периодами 2и 2' удовлетворяет соотношению

f(z) = f(K-z), (7)

где К - некоторое постоянное, то числа

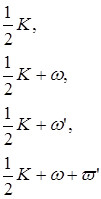
будут нули или полюсы производной f '( z ) . Действительно, дифференцируя соотношение (7), мы видим, что производная f '( z ) удовлетворяет соотношению вида (6), откуда и следует наше утверждение вследствие утверждения 1.

В частности, если К равно нулю, т. е. если f(z) - четная функция, то ее производная будет нечетной и будет иметь нули или полюсы в точках, изображающих периоды и полупериоды. Приложим теперь эти утверждения к эллиптическим функциям второго порядка.

Обозначим через и полюсы такой функции, расположенные в параллелограмме периодов. Пусть сначала неравно , т. е. оба полюса простые. В силу теоремы 5, если

то

,

откуда вытекает соотношение вида (7):

следовательно, по утверждению 1 точки

(8)

будут нулями или полюсами производной f '( z ) . С другой стороны, мы знаем полюсы производной f '( z ) ; она имеет в точках и полюсы второго порядка. Так как, очевидно, точки и не будут конгруэнтными с точками (8), то производная f '( z ) должна обращаться в нуль во всех четырех точках (8). Образуем теперь функцию

которая будет эллиптической с теми же периодами, что и f(z) , восьмого порядка; эта функция имеет два полюса четвертого порядка в точках и и нули второго порядка в четырех точках (8).

Последнее заключение сделано потому, что в точках (8) функция F ( z ) обращается в нуль вместе со своей производной. Заметив, что есть эллиптическая функция с теми же периодами, что и F (z), того же порядка и с теми же нулями и полюсами, мы на основании теоремы 2 (следствие 2) заключаем:

Откуда

(9)

Полагая