Курсовая работа: Уравнения смешанного типа

(0.8)

; (0.9)

(0.10)

(0.11)

где и – заданные достаточно гладкие функции, причём

, ,

Для указанных задач установлены критерии их однозначной разрешимости. Решения получены явно в виде соответствующих рядов.

1. Нелокальная граничная задача Ι рода

Рассмотрим вырождающееся уравнение смешанного типа

(1)

где в прямоугольной области заданные положительные числа, и для него исследуем следующую нелокальную задачу.

Задача 1. Найти в области функцию , удовлетворяющую условиям:

; (2)

; (3)

(4)

(5)

где и заданные достаточно гладкие функции, причём

Пусть решение задачи (2) Рассмотрим функции

(6)

(7)

(8)

Дифференцируя дважды равенство (8), учитывая уравнение (1) и условия (4), получим дифференциальное уравнение

(9)

с граничными условиями

, (10)

(11)

Общее решение уравнения (9) имеет вид

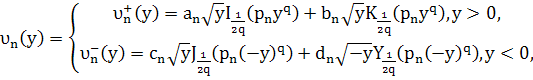
где и функции Бесселя первого и второго рода соответственно,модифицированные функции Бесселя, и произвольные постоянные,