Курсовая работа: Уравнения смешанного типа

Далее вычислим производную

Оценим эту функцию при и больших :

(41)

При и больших фиксированных имеем

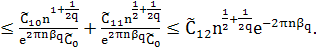(42)

Из оценок (41) и (42) следует, что при всех

Вторую производную функции вычислим следующим образом:

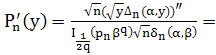
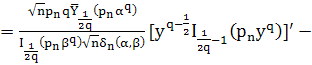
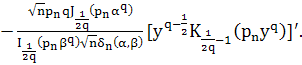
Используя формулы ([1], стр. 90)

Получаем

Зная оценку (40) для из последнего равенства при всех имеем

Функция с учётом (36) примет вид:

.

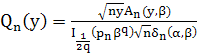Оценим её, используя лемму 1 при 0 и больших n:

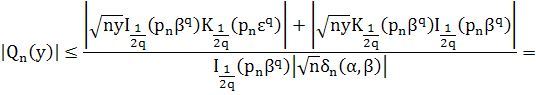
(43)

При и больших фиксированных :

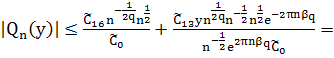
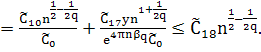(44)