Курсовая работа: Уравнения смешанного типа

Решение задачи (24) и (25) будет иметь вид

(26)

Аналогично для функции получаем неоднородное уравнение

(27)

с граничными условиями

(28)

(29)

Общее решение уравнения (27) имеет вид

Равенства будут выполняться при следующих значениях постоянных

,

при любых и Подставим выражения для постоянных и в (30), тогда функции примут вид

(31)

Для нахождения и на основании (28) и (29) получим систем

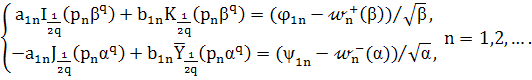(32)

Если выполнено условие (16), то и определяются по формулам:

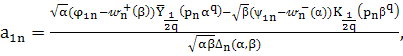(33)

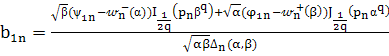, (34)

Найденные значения и по формулам (33) и (34) подставим в (31), тогда функции будут однозначно построены в явном виде:

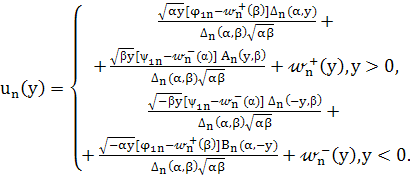(35)

Из формул (19), (26), (35) следует единственность решения задачи (2)так как если на , то , для на Тогда из (6) имеем:

Отсюда в силу полноты системы