Курсовая работа: Уравнения смешанного типа

Доказательство. Используя и функцию , определяемую формулой (19), представим в следующем виде:

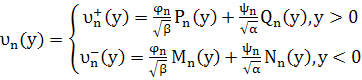(49)

Из (49) в силу леммы 2 получим оценки для функций и Аналогичные оценки справедливы и для функций и Лемма доказана.

Лемма 4. Пусть то справедливы оценки:

(50)

При получении оценок (50) дополнительно применяется теорема о скорости убывания коэффициентов ряда Фурье функции, удовлетворяющей на условию Гёльдера с показателем

Теорема 2. Пусть и выполнены условия (16) и (37). Тогда задача (2)-(5) однозначно разрешима и это решение определяется рядом

(51)

где функции , определены соответственно по формулам (26), (35), (19).

Доказательство. Поскольку системы функций

образуют базис Рисса, то если , тогда функцию можно представить в виде биортогонального ряда (51), который сходится в при любом . В силу лемм 3 и 4 ряд (51) при любом из мажорируется сходящимся рядом

поэтому ряд (51) в силу признака Вейерштрасса сходится абсолютно и равномерно в замкнутой области . Следовательно, функция непрерывна на как сумма равномерно сходящегося ряда (51). Ряды из производных второго порядка в мажорируются также сходящимся числовым рядом

Поэтому сумма ряда (51) принадлежит пространству и удовлетворяет уравнению (1) в . Следствие 1. Построенное решение задачи (2)-(5) принадлежит классу и функция всюду в является решением уравнения (1). Следовательно, линия изменения типа уравнения (1) как особая линия устраняется.

2. Нелокальная граничная задача II рода

Рассмотрим уравнение (1) в прямоугольной области и исследуем сопряжённую относительно задачи 1 задачу.

Задача 2. Найти в области функцию , удовлетворяющую условиям:

(52)

; (53)

(54)

(55)

где и – заданные достаточно гладкие функции, причём , ,

Пусть решение задачи (52)- (55). Вновь воспользуемся системами