Курсовая работа: Уравнения смешанного типа

Рассмотрим функции

, (56) (57)

(58)

Дифференцируя дважды равенство (56) и учитывая уравнение (1), получим дифференциальное уравнение

(59)

с граничными условиями

(60)

(61)

Следуя §1 решение задачи (59)-(61) построим в виде

(62)

C учётом уравнения (1) продифференцируем дважды равенство (57). Получим для функции однородное дифференциальное уравнение

(63)

с граничными условиями

(64)

Решение задачи (63) и (64) имеет вид

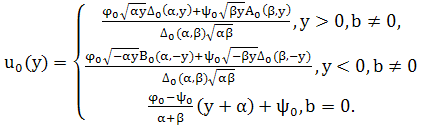(65)

Дифференцируя дважды равенство (58) и учитывая уравнение (1) и условия (54), получаем неоднородное уравнение для функции

(66)

с граничными условиями

, (67)

. (68)

Решение этой задачи определяется по формуле

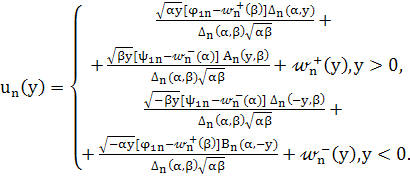(69)

Из формул (62), (65), (69) следует единственность решения задачи (52)-(55), так как если на то , , для на Тогда из (56)-(58) имеем:

, ,

Отсюда в силу полноты системы