Курсовая работа: Уравнения смешанного типа

Теорема 3. Если существует решение задачи (52)-(55), то оно единственно тогда и только тогда, когда при всех n выполняется условие (16).

Действительно, если выполнено условие (16) и решение задачи (52)-(55) существует, то оно единственно. Пусть при некоторых и нарушено условие (16), т. е. . Тогда однородная задача (52)-(55) (где ) имеет нетривиальное решение

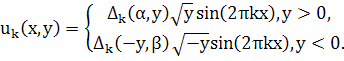
Теорема 4. Если , и выполнены условия (16) и (37), то существует единственное решение задачи (52)-(55) и оно представимо в виде суммы ряда

где функции , определены соответственно по формулам (65), (62), (69).

Доказательство теоремы 4 аналогично доказательству теоремы 2.

Следствие 2. Построенное решение задачи (52)-(55) принадлежит классу и функция всюду в является решением уравнения (1). Следовательно, линия изменения типа уравнения (1) как особая линия устраняется.

Литература

1. Бейтмен, Г. Высшие трансцендентные функции / Г. Бейтмен, А. Эрдейн.М.: Наука, 1966. Т.

2. Берс, Л. Математические вопросы дозвуковой и околозвуковой газовой динамики / Л. Берс. М.: ИЛ,

3. Бицадзе, А.В. О некоторых простейших обобщениях эллиптических задач/ А.В. Бицадзе, А.А. Самарский // Докл. АН СССР. – 1969. – Т. 185. – № 4. – С. 739 – 740.

4. Бицадзе, А.В. Некоторые классы уравнений в частных производных /

А.В. Бицадзе. – М.: Наука, 1981.– 448 с.

5. Ватсон, Г.Н. Теория бесселевых функций.I./ Г.Н. Ватсон.–М.: ИЛ, 1940.– 421 с.

6. Гудерлей, К.Г. Теория околозвуковых течений / К.Г. Гудерлей. – М.: ИЛ, 1960. – 421 с.

7. Джураев, Т.Д. Краевые задачи для уравнений смешанного и смешанно-составного типов /Т.Д. Джураев – М.: ИЛ, 1961. – 208 с.

8. Жегалов, В.И. Нелокальная задача Дирихле для уравнения смешанного типа / В.И. Жегалов // Неклассич. уравнения матем. физики. – Новосибирск: ИМ СО АН СССР. 1985. – С.172 с.

9. Моисеев, Е.И. Уравнения смешанного типа со спектральным параметром / Е.И. Моисеев. – М.: МГУ, 1988. – 150 с.

10. Пулькина, Л.С. Нелокальная задача с нелокальным условием для гиперболического уравнения / Л.С. Пулькина // Неклассич. уравнения матем. физики. Новосибирск: ИМ СО РАН, 2002. – С. 176 – 184 с.

11. Репин, О.А. Задача Трикоми для уравнения смешанного типа в области, эллиптическая часть которой – полуполоса / О.А. Репин // Дифференциальные уравнения. – 1996. – Т. 32, №4. – С. 565 – 567 с.

12. Сабитов, К.Б. К теории уравнений смешанного типа с двумя линиями изменения типа / К.Б. Сабитов, Г.Г. Биккулова, А.А. Гималтдинова – Уфа.: Гилем, 2006. – 150 с.

13. Салахитдинов, М.С. Уравнения смешанно-составного типа – М.С. Салахитдинов. – Ташкент: Фан, 1974. – 156 с.

14. Смирнов, М.М. Уравнения смешанного типа / М.М Смирнов. – М.: Высшая школа, 1985. – 304 с.

15. Франкль, Ф.И. Обтекание профилей потоком дозвуковой скорости со сверхзвуковой зоной, оканчивающейся прямым скачком уплотнения / Ф.И. Франкль // ПММ. – 1956. – Т. 20. – №2. – с. 196 –202 с.