Курсовая работа: Уравнения смешанного типа
Таким образом, нами доказана следующая
Теорема 1. Если существует решение ![]() задачи (2)
задачи (2)![]() то оно единственно только тогда, когда
то оно единственно только тогда, когда ![]() при всех
при всех ![]()
Действительно, если выполнено условие (16) и решение задачи (2)![]() существует, то оно единственно. Пусть при некоторых
существует, то оно единственно. Пусть при некоторых ![]() и
и ![]() нарушено условие (16), т. е.
нарушено условие (16), т. е. ![]() Тогда однородная задача (2)
Тогда однородная задача (2)![]() (где
(где ![]() имеет нетривиальное решение
имеет нетривиальное решение
![]()
Выражение для ![]() на основании следующих формул
на основании следующих формул
![]()
приводим к виду
![]()
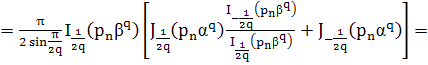
![]()
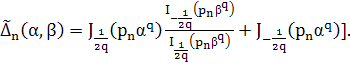
Поскольку при любом ![]() и
и ![]()
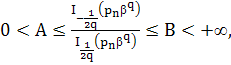
где ![]() и
и ![]() положительные постоянные, то функция
положительные постоянные, то функция
![]()
где ![]() в силу теоремы Хилби
в силу теоремы Хилби ![]() имеет счётное множество положительных нулей.
имеет счётное множество положительных нулей.
Следовательно, ![]() при некоторых
при некоторых ![]() может иметь счётное множество нулей независимо от
может иметь счётное множество нулей независимо от ![]() . Поскольку
. Поскольку ![]() любое положительное число ,то оно может принимать значения, близкие к нулям
любое положительное число ,то оно может принимать значения, близкие к нулям ![]() Поэтому при больших n выражение
Поэтому при больших n выражение![]() может стать достаточно малым, т.е. возникает проблема
может стать достаточно малым, т.е. возникает проблема ![]() Чтобы такой ситуации не было, надо показать существование
Чтобы такой ситуации не было, надо показать существование ![]() и
и ![]() таких, что при любом
таких, что при любом ![]() и больших
и больших ![]() справедлива оценка
справедлива оценка
![]()
Представим (16) в следующем виде
![]() (36)
(36)
где

Как известно ![]() функция
функция ![]() строго убывает, функция
строго убывает, функция ![]() строго возрастающая по
строго возрастающая по ![]() , поэтому величина
, поэтому величина

есть бесконечно малая более высокого порядка, чем ![]() при больших
при больших ![]() . Поэтому рассмотрим только выражение
. Поэтому рассмотрим только выражение
![]()
Используя асимптотическую формулу функции ![]() при
при ![]()

Получаем