Курсовая работа: Застосування симетричних многочленів

а тому для нових невідомих отримуємо наступну систему рівнянь:

З цієї системи рівнянь отримуємо .

Отже, тобто для первинних невідомих x, y ми отримуємо наступну систему рівнянь :

Ця система рівнянь легко розв’язується, і ми отримуємо наступний розв’язок первинної системи:

Приклад 2. Розв’язати систему рівнянь

Розв’язання проводиться аналогічно. Вважаючи, що приводимо початкову систему до вигляду

Звідси для отримуємо квадратне рівняння

Чи

З цього рівняння знаходимо два значення для:

Таким чином, для первинних невідомих x, y отримуємо дві системи рівнянь:

та Розв’язавши ці системи, знаходимо чотири розв’язки первинної системи:

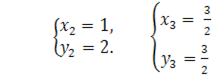
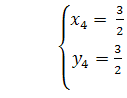
2.2 Доведення тотожностей

У цілому ряді завдань на доведення тотожності також з успіхом можуть бути застосовані елементарні симетричні многочлени. За основною теоремою симетричних многочленів, кожну степеневу суму можна представити у вигляді многочлена від,

Таблиця 2. 1 Вирази степенних сум через,

Кожну степеневу суму можна представити у вигляді многочлена від , , за умови, що .

Таблиця 2.2 Вирази степенних сум через при виконанні умови

Існують одночлени, які не змінюються при перестановці змінних – симетричні одночлени. Легко побачити, що усі змінні в такий одночлен повинні входити в одному і тому ж степені, тобто цей одночлен повинен збігатися з добутком (взятий з деяким числовим коефіцієнтом).

Якщо показники степеня одночлена є різними то цей одночлен не є симетричним. Щоб отримати симетричний одночлен, одним із доданків, якого є, необхідно додати до нього інші одночлени.

Позначимо через O – многочлен з найменшим числом членів, одним із доданків, якого є одночлен, цей многочлен має назву орбіта.

Для отримання орбіти одночлена необхідно додати до нього одночлени отримані за допомогою перестановок змінних x, y, z. Якщо три показники степеня (k, l, m ) не рівні між собою, то орбіта O( буде складатися з шести членів. Наприклад: