Реферат: Экзаменационные вопросы и билеты по линейной алгебре за весенний семестр 2001 года
примерный перечень экзаменационных вопросов
линейная алгебра
1. Прямоугольная матрица, ее порядок, главная и побочная диагонали. Единичная, нулевая, треугольная, симметричная, транспонированная матрицы. Примеры.
2. Сложение матриц, умножение матрицы на число, умножение матриц. Свойства ассоциативности и коммутативности матриц. Примеры.
3. Приведение матриц к ступенчатому виду методом Гаусса. Элементарные преобразования над строками матрицы. Пример. Ранг матрицы.
4. Система из “m” линейных уравнений с “n” неизвестными. Векторно-матричная форма записи. Расширенная матрица системы. Пример.
5. Однородные и неоднородные системы уравнений. В каком случае они имеют единственное решение? Пример.
6. Решение однородной и неоднородной систем методом Гаусса. Пример.
7. Однородные системы и их свойства. Эквивалентные системы.
8. Свободные и несвободные переменные однородной системы. Частное и общее решение. Пример.
9. Совместные системы уравнений. Теорема Кронекера-Капелли. Пример.
10. Вектор решения линейной системы уравнений. Общее и частное решение неоднородной системы уравнений. Основные свойства решений.
11. Модель Леонтьева межотраслевого баланса. Ее математическая модель.
12. Определитель матрицы. Его порядок. Понятие определителя применительно к матрицам второго и третьего порядков. Алгебраическое дополнение элемента. Разложение определителя по строке или столбцу.
13. Сформулировать свойства определителя.
14. Какую матрицу называют обратной? Условие ее существования.
15. Вычисление определителя с использованием метода Гаусса.
16. Построение обратной матрицы с использованием алгебраических дополнений и методом Гаусса.
17. Даны матрицы А=
и В=
. Найти АВ - ВА.
18. Найти ранг матрицы: 
A =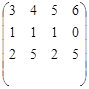
.
19. Найти ранг матрицы 
.
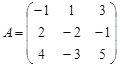20. Исследовать сколько решений может иметь система уравнений: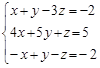 
.
21. Найти общее решение однородной системы: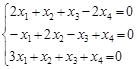 
.
22. Исследовать и решить в случае совместности систему уравнений: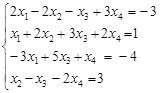 
.
23. Вычислить определитель матрицы det A, где А =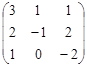 
методом Гаусса.
24. Что называется линейным пространством? Элемент линейного пространства. Какое множество функций на отрезке [ a , b ] образует пространство C [ a , b ] ?
25. Свойства коммутативности и ассоциативности сложения векторов.
26. Арифметическое пространство Rn . Что называют компонентами вектора?
27. Определите понятие подпространства Н в пространстве V . Приведите примеры линейных подпространств в линейном пространстве V , в пространстве Rn .
28. Определите понятие линейной комбинации векторов u иv линейного пространства. Какая система векторов называется линейно независимой?
--> ЧИТАТЬ ПОЛНОСТЬЮ <--