Реферат: Экзаменационные вопросы и билеты по линейной алгебре за весенний семестр 2001 года

95. Запишите матрицу перехода от базиса b к новому с , если b₁ =-с₁ -7с₂ +2с₃ , b₂ =-9с₁ + 8с₂ -с₃ , b₃ =с₁ +2с₂ +5с₃ .

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 21

96. Какое решение неоднородной системы линейных уравнений называют общим? Какое – частным?

97. Сколько решений может иметь система уравнений:?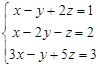

98. Запишите свойства линейно независимой системы векторов.

99. Что можно сказать об операторе А , если известно, что его матрица в некотором ортонормированном базисе является симметрической?

100. Что можно сказать о собственных векторах, если они соответствуют различным собственным значениям?

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 22

101. Построение обратной матрицы с использованием метода Гаусса (на примере).

102. Вычислить определитель матрицы detA, где А = 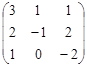методом Гаусса.

103. В каком случае совпадают матрицы двух различных линейных операторов?

104. В каком базисе матрица линейного оператора А является диагональной?

105. Является ли линейно зависимой система векторов а =(5,4,3), b =(3,3,2), с =(8,1,3)?

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 23

106. Основные свойства определителя.

107. Сколько решений может иметь система уравнений: ?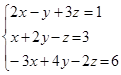

108. Какой вид имеет матрица перехода от старого базиса к новому, если матрица перехода от нового базиса к старому является треугольной?

109. Запишите квадратичную форму в координатах в некотором базисе.

110. Может ли матрица А =быть матрицей перехода от одного базиса трехмерного пространства к другому?

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 24

111. Чему равен определитель треугольной матрицы? Меняют ли элементарные преобразования величину определителя? В каком случае определитель матрицы не равен нулю?

112. Исследовать и решить в случае совместности систему уравнений: .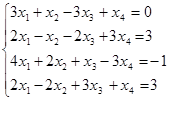

113. Запишите формулы преобразования координат вектора х линейного пространства L при переходе от старого базиса b к новому с .

114. Какова матрица самосопряженного оператора в ортонормированном базисе?

115. Запишите матрицу перехода от базиса b к новому с , если b₁ = 4с₁ -5с₂ +с₃ , b₂ =с₁ -3с₂ -2с₃ , b₃ =5с₁ +с₂ +с₃ .

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 25

116. Какое решение однородной системы уравнений называют общим, частным? Пример.

117. Найти матрицу А^-1 , обратную к матрице А и с ее помощью решить систему А = , где А = , = , .

118. Какое множество функций на отрезке [a,b] образует пространство С_[a,b] ?

119. Дайте определение понятия собственного числа линейного оператора А .

120. Определите, каким является базис а =(1/, 1/,1/), b =(1/, -1/, 0), с =(1/, 1/,-2/).

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 26

121. Приведение матрицы к ступенчатому виду методом Гаусса. Пример.

122. Вычислить определитель матрицы detA, где А = методом Гаусса.

123. Образует ли линейное пространство множество функций, непрерывных на отрезке [a,b], относительно операций сложения функций и умножения функции на число?