Реферат: Экзаменационные вопросы и билеты по линейной алгебре за весенний семестр 2001 года

60. Дайте понятие линейного оператора, действующего в линейном пространстве L . Приведите примеры.

61. Какая матрица называется матрицей линейного оператора?

62. Какую матрицу имеет нулевой оператор, действующий в пространстве L ? Какой вид у матрицы тождественного оператора, действующего в пространстве L ?

63. Сформулируйте теорему о связи координат вектора-прообраза с координатами вектора-образа оператора А , действующего в пространстве L ?

64. В каком случае совпадают матрицы двух различных линейных операторов?

65. Какое соответствие существует между квадратными матрицами порядка n и линейными операторами, действующими в n - мерном линейном пространстве?

66. Напишите зависимость, связывающую матрицы А_b и А_е в различных базисах b и e линейного пространства.

67. Определение характеристического уравнения матрицы А.

68. Дайте определение понятия собственное число линейного оператора А . Какой вектор называется собственным вектором оператора? Как его найти?

69. Что означает понятие «собственное подпространство», отвечающее данному собственному значению?

70. Составьте характеристическое уравнение для оператора А , если его матрица А=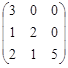. Найдите собственные значения и собственные векторы линейного оператора А.

71. Скольким собственным значениям может соответствовать один и тот же собственный вектор?

72. Известно, что собственные значения l₁ , l₂ ,..,l_n линейного оператора попарно различны. Что можно сказать о линейной зависимости соответствующей им системы собственных векторов?

73. Известно, что базис е состоит из собственных векторов оператора А . Что можно сказать о матрице оператора в этом базисе?

74. Когда матрица оператора А подобна некоторой диагональной?

75. Пусть l₁ , l₂ ,.., l_n - собственные значения оператора А . Найдите собственные значения линейного оператора, матрицей которого является матрица А² , А^-1 .

76. Дайте определение оператора, сопряженного к данному линейному оператору А . Сколько сопряженных операторов может быть у оператора А в евклидовом пространстве?

77. Какая матрица является матрицей оператора сопряженного линейному оператору А с матрицей А в ортонормированном базисе?

78. Дайте определение самосопряженного оператора. Приведите пример самосопряженного оператора.

79. Какова матрица самосопряженного оператора в ортонормированном базисе?

80. Что можно сказать об операторе А , если известно, что его матрица в некотором ортонормированном базисе является симметрической?

81. Каковы корни характеристического уравнения самосопряженного оператора?

82. Сколько собственных значений имеет симметрическая матрица порядка n ?

83. Каким свойством обладают собственные векторы самосопряженного оператора?

84. Когда в евклидовом пространстве существует ортонормированный базис, в котором матрица линейного оператора имеет диагональный вид?

85. Докажите, что (А+ В)^* = А^* + В^* и (АВ)^* = В^* А^* .

86. В ортонормированном базисе оператор А имеет матрицу А = 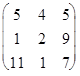. Найдите матрицу сопряженного ему оператора в этом же базисе.

87. Какая матрица называется ортогональной матрицей и чему равен ее определитель?

88. Свойства ортогональных матриц.