Реферат: Экзаменационные вопросы и билеты по линейной алгебре за весенний семестр 2001 года
5. Запишите матрицу перехода от базиса b к новому с , если b1 =3с1 -с2 +2с3 , b2 =-6с1 +5с2 -2с3 , b3 =4с1 +с2 -с3 .
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 3
6. Дать определение системы из «m» линейных уравнений с «n» неизвестными. Векторно-матричная форма записи системы линейных уравнений.
7. Исследовать и решить в случае совместности систему уравнений: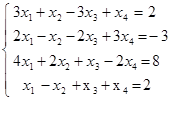 
.
8. Дайте определение понятия арифметического пространства Rn .
9. Какой матрицей является матрица, транспонированная к ортогональной?
10. Докажите, что для любых двух векторов а и с векторное уравнение а+х = с относительно х имеет решение, и притом единственное.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 4
11. Какой метод используется при решении системы линейных уравнений (на примере)?
12. Исследовать и решить в случае совместности систему уравнений: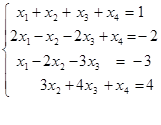 
.
13. Запишите свойства линейно зависимой системы векторов.
14. Дайте определение Гессиана.
15. Составьте Гессиан для функции f ( x1 ,....,xn )= x1 2 +x 1 x 2 + .... + x 1 x n .
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 5
16. Неоднородные системы уравнений. Основные свойства решений.
17. Найти матрицу 
А-1 , обратную к матрице А и с ее помощью решить систему А
= 
, где А = 
,=
, 
.
18. Сформулируйте теорему о связи координат вектора-прообраза с координатами вектора-образа оператора А , действующего в пространстве L .
19. Какая матрица является матрицей оператора сопряженного линейному оператору А с матрицей А в ортонормированном базисе?
20. Выясните, является ли квадратичная форма с матрицей А =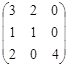 
положительно определенной.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 6
21. Правило построения обратной матрицы на примере матрицы 2-го порядка с использованием алгебраических дополнений.
22. Совместна ли система уравнений: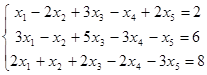
?
23. Выясните, образует ли линейное пространство множество всех векторов данной плоскости, не параллельных данной прямой, если в качестве операций взяты операции сложения векторов и умножения вектора на число.
24. Скольким собственным значениям может соответствовать один и тот же собственный вектор?
25. Составьте Гессиан для функции f ( x1 ,....,xn )= x1 2 + 2x2 2 + .... + nxn 2 .
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 7
26. Что называют определителем матрицы. Порядок определителя. Понятие определителя применительно к матрице второго порядка. Пример.
27. Найти ранг матрицы 
.
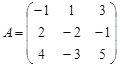28. Как записывается свойство коммутативности сложения векторов?
29. Какую квадратичную форму можно привести к каноническому виду?
30. Найдите ранг квадратичной формы трех переменных х2 + у 2 +2хz.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 8
31. Подчиняется ли умножение матриц свойству ассоциативности и перестановки сомножителей? Привести пример некоммунитативных матриц. Пример перестановочных матриц.
32. Найти общее решение однородной системы: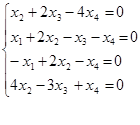 
.
33. Что называется линейным пространством?