Реферат: Экзаменационные вопросы и билеты по линейной алгебре за весенний семестр 2001 года

35. В ортонормированном базисе оператор А имеет матрицу А =. Найдите матрицу сопряженного ему оператора в этом же базисе.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 9

36. Дать определение ранга матрицы. Пример.

37. Убедиться, что система имеет единственное решение, и найти это решение методом Гаусса: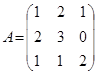
, , .

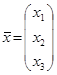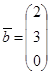38. Какая система векторов называется линейно независимой?

39. Какой матрицей будет матрица, обратная к ортогональной?

40. Докажите, что (А+ В)^* = А^* + В^* .

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 10

41. Какие преобразования можно выполнить над строками матрицы? Пример.

42. Найти общее решение однородной системы уравнений .

43. Какой базис линейного пространства называется ортогональным?

44. Сколько сопряженных операторов может быть у оператора А в евклидовом пространстве?

45. Чему равно скалярное произведение векторов в арифметическом пространстве Rⁿ ?

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 11

46. При решении однородной системы какие переменные называют свободными, а какие несвободными? Чему равно число свободных переменных?

47. Исследовать и решить в случае совместности систему уравнений: .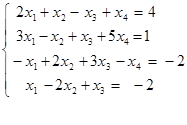

48. Докажите, что множество матриц-столбцов высоты n образует линейное пространство относительно матричных операций сложения и умножения на число.

49. Сколько собственных значений имеет симметрическая матрица порядка n?

50. Запишите матрицу перехода от базиса b к новому с , если b₁ =-2с₁ -3с₂ -2с₃ , b₂ =7с₁ +8с₂ +9с₃ , b₃ =3с₁ +4с₂ +5с₃ .

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 12

51. Элементарные преобразования над строками матрицы. Пример.

52. Убедиться, что система , имеет единственное решение, и найти это решение методом Гаусса: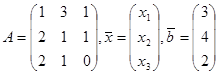
.

53. Для каких векторов евклидова пространства неравенство Коши – Буняковского превращается в равенство?

54. Чему равна матрица, обратная к ортогональной?

55. Найдите ранг квадратичной формы трех переменных 2ху+ 2уz +2хz.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 13

56. Решение однородной системы методом Гаусса. Пример.

57. Найти матрицу А^-1 , обратную к матрице А и с ее помощью решить систему А = , где А = ,=, .

58. Определите понятие подпространства Н в пространстве V.

59. Дайте понятие матрицы квадратичной формы.

60. Какой нормированный вектор соответствует вектору х = -5i + 3j + 7k ?

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 14

61. Какую систему уравнений называют неоднородной? В каком случае она имеет единственное решение?

62. Найти матрицу А^-1 , обратную к матрице .

63. Что называется разложением вектора по базису?