Реферат: Экзаменационные вопросы и билеты по линейной алгебре за весенний семестр 2001 года
90. Запишите квадратичную форму в координатах в некотором базисе.
91. Что такое канонический вид квадратичной формы? Найти ее для x2 + xy + y2 .
92. Какая квадратичная форма называется положительно определенной? Неотрицательно определенной?
93. Сформулируйте критерий Сильвестра.
94. Запишите закон инерции для квадратичной формы.
95. Что представляет собой метод итераций?
96. Дайте определение Гессиана.
97. Составьте Гессиан для функции f ( x1 ,....,xn )= x1 2 +x 1 x 2 + .... + x 1 x n .
98. Приведите квадратичную форму х1 2 - 4х1 х2 к каноническому виду методом выделения квадратов.
99. Какую квадратичную форму можно привести к каноническому виду?
100. Как изменяется характеристическое уравнение матрицы при ортогональном преобразовании квадратичной формы?
101. Выясните, является ли квадратичная форма с матрицей А =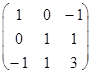 
положительно определенной?
102. Когда диагональные элементы симметрической матрицы ― положительные числа?
103. Найдите ранг квадратичной формы трех переменных 2ху+ 2уz +2хz.
104. Какой ранг может иметь положительно определенная форма от n переменных?
105. Запишите матрицу перехода от базиса е к базису е ¢ , если е ¢ 1 = е1 + е2 +7е3 , е ¢ 2 =(7/6) е1 - е2 , е ¢ 3 =- е1 + е2 + е3 .
106. Является ли линейным преобразование Ах = (6х1 - 5х2 ,-2х2 , х3 - х1 )?
107. Чему равно скалярное произведение векторов в арифметическом пространстве Rn ?
108. Что можно сказать о собственных векторах, если они соответствуют различным собственным значениям?
109. Определите, каким является базис а =(1/
, 1/,1/), b =(1/
, -1/, 0), с =(1/
, 1/,-2/).
110. Нормируйте вектор х = 3i + 4j + 5k + 7m .
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 1
1. Описать модель Леонтьева межотраслевого баланса.
2. Найти общее решение однородной системы: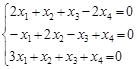 
.
3. Как записывается свойство ассоциативности сложения векторов?
4. Когда в евклидовом пространстве существует ортонормированный базис, в котором матрица линейного оператора имеет диагональный вид?
5. В ортонормированном базисе оператор А имеет матрицу А =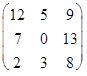
. Найдите матрицу сопряженного ему оператора в этом же базисе.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 2
1. Какие прямоугольные матрицы можно привести к ступенчатому виду? Метод приведения матрицы к ступенчатому виду. Пример.
2. Найти матрицу 
А-1 , обратную к матрице А и с ее помощью решить систему А
= 
, где А =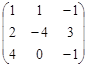 
, = 
, 
.
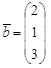3. Образует ли линейное пространство множество многочленов степени n относительно обычных операций сложения многочленов и умножения многочлена на число?