Реферат: Геометрические и физические приложения двойных, тройных, криволинейных и поверхностных интеграло

где D (u,v ) − это область, в которой задана поверхность.

Если поверхность S задана в явном виде функцией z (x,y ), то площадь поверхности выражается формулой

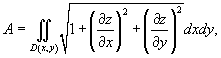
где D (x,y ) − проекция поверхности S на плоскость xy .

Объем тела, ограниченного замкнутой поверхностью

Предположим, что тело ограничено некоторой гладкой, замкнутой поверхностью S . Тогда объем тела определяется по формуле

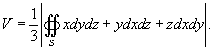
Пример

Вычислить площадь поверхности части параболоида , лежащей выше плоскости xy .

Площади заданной поверхности равна

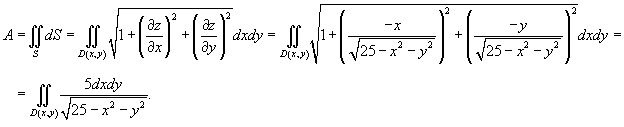
Переходя к полярным координатам, находим ответ:

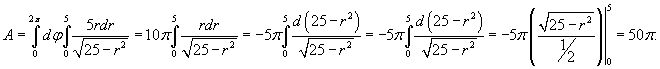
2. Физические приложения интегралов

2.1Физические приложения двойных интегралов

Масса и статические моменты пластины

Предположим, что плоская пластина изготовлена из неоднородного материала и занимает область R в плоскости Oxy . Пусть плотность пластины в точке (x, y ) в области R равна . Тогда масса пластины выражается через двойной интеграл в виде

Статический момент пластины относительно оси Ox определяется формулой

Аналогично находится статический момент пластины относительно оси Oy :

Координаты центра масс пластины , занимающей область R в плоскости Oxy с плотностью, распределенной по закону , описываются формулами

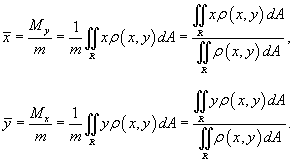
Для однородной пластины с плотностью для всех (x, y ) в области R центр масс определяется только формой области и называется центроидом .

Моменты инерции пластины

Момент инерции пластины относительно оси Ox выражается формулой

Аналогично вычисляется момент инерции пластины относительно оси Oy :