Реферат: Геометрические и физические приложения двойных, тройных, криволинейных и поверхностных интеграло
![]()
Моментом инерции тела относительно начала координат называется интеграл
![]()
Момент инерции относительно начала координат можно выразить через моменты инерции относительно координатных плоскостей:
![]()
Тензор инерции
Используя рассмотренные выше 6 чисел Ix , Iy , Iz , Ixy , Ixz , Iyz , можно составить так называемую матрицу инерции или тензор инерции тела:
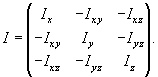
Данный тензор является симметричным, и, следовательно, его можно привести к диагональному виду при определенном выборе осей Ox', Oy', Oz' . Значения диагональных элементов (после приведения тензора к диагональному виду) называются главными моментами инерции , а указанные направления − собственными векторами или главными осями инерции .
Если тело вращается вокруг оси, не совпадаюшей с главной осью инерции, то оно будет испытывать вибрации при высоких скоростях вращения. Поэтому, при конструировании таких устройств необходимо, чтобы ось вращения совпадала с одной из главных осей инерции. Например, при замене шин автомобиля проводится их балансировка: небольшие грузики добавляются к колесам, чтобы обеспечить совпадение оси вращения с главной осью инерции и исключить вибрации.
Гравитационный потенциал и сила тяготения
Ньютоновым потенциалом тела в точке P (x,y,z ) называется интеграл
![]()
где ρ (ξ,η,ζ ) − плотность тела, и ![]() .
.
Интегрирование выполняется по всему объему тела. Зная потенциал, можно вычислить силу притяжения материальной точки массы m и заданного распределенного тела с плотностью ρ (ξ,η,ζ ) по формуле
![]()
где G − гравитационная постоянная.
Пример
Найти массу шара радиуса R , плотность γ которого пропорциональна квадрату расстояния от центра.
По условию, плотность γ задана соотношением γ = ar 2 , где a − некоторая постоянная, r − расстояние от центра. Массу шара удобно вычислить в сферических координатах:
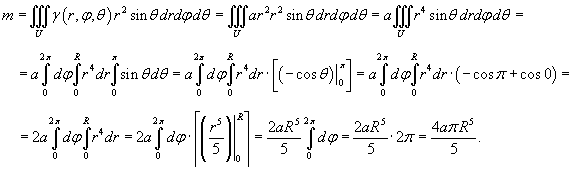
2.3 Физические приложения криволинейных интегралов
С помощью криволинейных интегралов вычисляются
1) Масса кривой;
2) Центр масс и моменты инерции кривой;
3) Работа при перемещении тела в силовом поле;
4) Магнитное поле вокруг проводника с током (Закон Ампера);
5) Электромагнитная индукция в замкнутом контуре при изменении магнитного потока (Закон Фарадея).
Рассмотрим эти приложения более подробно с примерами.