Реферат: Геометрические и физические приложения двойных, тройных, криволинейных и поверхностных интеграло

Предположим, что кусок проволоки описывается некоторой пространственной кривой C . Пусть масса распределена вдоль этой кривой с плотностью ρ (x,y,z ). Тогда общая масса кривой выражается через криволинейный интеграл первого рода

Если кривая C задана в параметрическом виде с помощью векторной функции , то ее масса описывается формулой

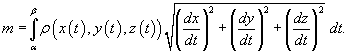
В случае плоской кривой, заданной в плоскости Oxy , масса определяется как

или в параметрической форме

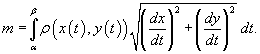
Центр масс и моменты инерции кривой

Пусть снова кусок проволоки описывается некоторой кривой C , а распределение массы вдоль кривой задано непрерывной функцией плотности ρ (x,y,z ). Тогда координаты центра масс кривой определяются формулами

где

− так называемые моменты первого порядка .

Моменты инерции относительно осей Ox, Oy и Oz определяются формулами

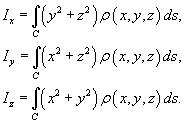
Работа поля

Работа при перемещении тела в силовом поле вдоль кривой C выражается через криволинейный интеграл второго рода

где − сила, действующая на тело, − единичный касательный вектор (рисунок 1). Обозначение означает скалярное произведение векторов и .

Заметим, что силовое поле не обязательно является причиной движения тела. Тело может двигаться под действием другой силы. В таком случае работа силы иногда может оказаться отрицательной.

Если векторное поля задано в координатной форме в виде

то работа поля вычисляется по формуле

В частном случае, когда тело двигается вдоль плоской кривой C в плоскости Oxy , справедлива формула

Где

Если траектория движения C определена через параметр t (t часто означает время), то формула для вычисления работы принимает вид

где t изменяется в интервале от α до β . Если векторное поле потенциально , то работа по перемещению тела из точки A в точку B выражается формулой

где − потенциал поля.

Рис.1	Рис.2