Реферат: Геометрические и физические приложения двойных, тройных, криволинейных и поверхностных интеграло

Полярный момент инерции пластины равен

Заряд пластины

Предположим, что электрический заряд распределен по области R в плоскости Oxy и его плотность распределения задана функцией . Тогда полный заряд пластины Q определяется выражением

Среднее значение функции

Приведем также формулу дял расчета среднего значения некоторой распределенной величины. Пусть f (x,y ) является непрерывной функцией в замкнутой области R в плоскости Oxy . Среднее значение функции μ функции f (x,y ) в области R определяется формулой

где − площадь области интегрирования R .

Пример

Вычислить моменты инерции треугольника, ограниченного прямыми (рисунок 2) и имеющего плотность .

Найдем момент инерции пластины относительно оси Ox .

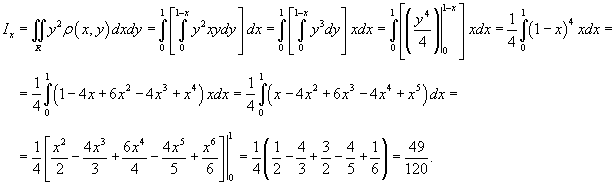
Аналогично вычислим момент инерции относительно оси Oy .

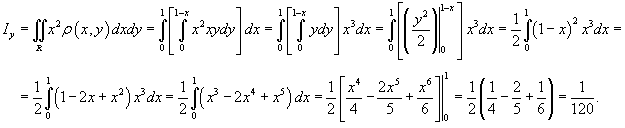
2.2 Физические приложения тройных интегралов

Масса и статические моменты тела

Пусть тело занимает объем U и его объемная плотность в точке M (x,y,z ) задана функцией ρ (x,y,z ). Тогда масса тела m вычисляется с помощью тройного интеграла:

Статические моменты тела относительно координатных плоскостей Oxy, Oxz, Oyz выражаются формулами

Координаты центра тяжести тела вычисляются по формулам:

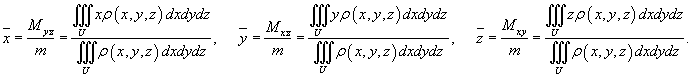
Если тело является однородным с плотностью ρ (x,y,z ) = 1 для точек M (x,y,z ) в области U , то центр тяжести тела зависит только от геометрии тела и называется центроидом .

Моменты инерции тела

Моменты инерции тела относительно координатных плоскостей Oxy, Oxz, Oyz определяются выражениями

а моменты инерции тела относительно координатных осей Ox, Oy, Oz вычисляются по формулам