Реферат: Классические методы безусловной оптимизации

Введение

Как известно, классическая задача безусловной оптимизации имеет вид:

(1)

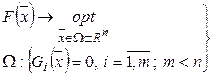(2)

Существуют аналитические и численные методы решения этих задач.

Прежде всего вспомним аналитические методы решения задачи безусловной оптимизации.

Методы безусловной оптимизации занимают значительное место в курсе МО. Это обусловлено непосредственным применением их при решении ряда оптимизационных задач, а также при реализации методов решения значительной части задач условной оптимизации (задач МП).

1. Необходимые условия для точки локального минимума (максимума)

Пусть т. доставляет минимальные значения функции . Известно, что в этой точке приращение функции неотрицательно, т.е.

. (1)

Найдем , используя разложения функции в окрестности т. в ряд Тейлора.

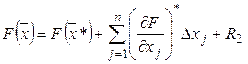, (2)

где 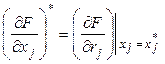, , - сумма членов ряда порядок которых относительно приращений (двум) и выше.

Из (2) имеем:

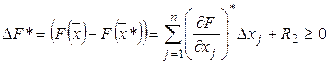(3)

Далее предположим, что изменяется только одна переменная из множества переменных . Например, , тогда (3) преобразуется к виду:

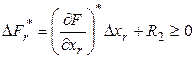(4)

Из (4) с очевидностью следует, что

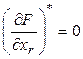(5)

Предположим, что 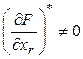, тогда

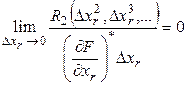(6)

С учетом (6) имеем: 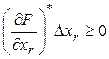. (7)

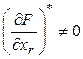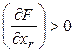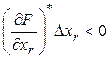Предположим, что положительно, т.е. . Выберем при этом , тогда произведение , что противоречит (1).

Поэтому, действительно, 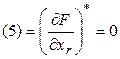очевиден.

Рассуждая аналогично относительно других переменных получаем необходимое условие для точек локального минимума функции многих переменных

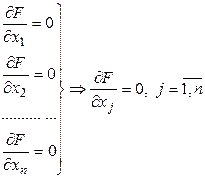(8)

Легко доказать, что для точки локального максимума необходимые условия будут точно такими же, как и для точки локального минимуму, т.е. условиями (8).

Понятно, что итогом доказательства будет неравенство вида: - условие неположительного приращения функции в окрестности локального максимума.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--