Реферат: Классические методы безусловной оптимизации

Позволяет ответить на вопрос: является ли квадратичная форма и матрица, ее представляющая, положительно определенной, или отрицательно определенной.

Далее изложение будет относительно ДКФ и матрицы ее определяющей, т.е. ДКФ вида

.

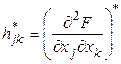, - называется матрицей Гессе.

Главный определитель матрицы Гессе

и ДКФ, которую оно представляет, будут положительно определенными, если все главные определители матрицы Гессе () положительны (т.е. имеет место следующая схема знаков:

)

Если же имеет место другая схема знаков для главных определителей матрицы Гессе , например, , то матрица и ДКФ отрицательно определены.

4. Метод Эйлера – классический метод решения задач безусловной оптимизации

Этот метод основан на необходимых и достаточных условиях, изученных в 1.1 – 1.3; применим нахождению локальных экстремумов только непрерывных дифференцируемых функций.

Алгоритм этого метода достаточно прост:

1) используя необходимые условия формируем систему в общем случае нелинейных уравнений. Отметим, что решить аналитически эту систему в общем случае невозможно; следует применить численные методы решения систем нелинейных уравнений (НУ) (см. "ЧМ"). По этой причине метод Эйлера будет аналитически-численным методом. Решая указанную систему уравнений находим координаты стационарной точки .;

2) исследуем ДКФ и матрицу Гессе , которая ее представляет. С помощью критерия Сильвестра определяем, является ли стационарная точка точкой минимума или точкой максимума;

3) вычисляем значение целевой функции в экстремальной точке

Методом Эйлера решить следующую задачу безусловной оптимизации: найти 4 стационарные точки функции вида:

Выяснить характер этих точек, являются ли они точками минимума, или Седловыми (см. [3]). Построить графическое отображение этой функции в пространстве и на плоскости (с помощью линий уровня).

Далее эту функцию будем именовать типовой функцией, исследуя ее экстремальные свойства всеми изученными методами.

5. Классическая задача условной оптимизации и методы ее решения: Метод исключения и Метод множителей Лагранжа (ММЛ)

Как известно, классическая задача условной оптимизации имеет вид:

(1)

(2)

График, поясняющий постановку задачи (1), (2) в пространстве .