Реферат: Классические методы безусловной оптимизации
Перепишем (8) в виде
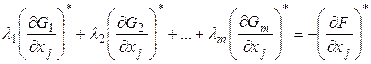 ,
, ![]() (8')
(8')
Система (8') представляет собой систему из ![]() линейных уравнений относительно
линейных уравнений относительно ![]() известных:
известных: ![]() . Система разрешима, если
. Система разрешима, если ![]() (вот почему, как и в методе исключения в рассматриваемом случае должно выполняться условие
(вот почему, как и в методе исключения в рассматриваемом случае должно выполняться условие ![]() ). (9)
). (9)
Поскольку в ключевом выражении (7) первая сумма равна нулю, то легко понять, что и вторая сумма будет равняться нулю, т.е. имеет место следующая система уравнений:
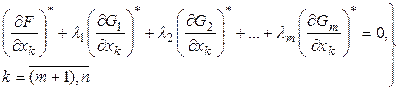 (10)
(10)
Система уравнений (8) состоит из ![]() уравнений, а система уравнений (10) состоит из
уравнений, а система уравнений (10) состоит из ![]() уравнений; всего
уравнений; всего ![]() уравнений в двух системах, а неизвестных
уравнений в двух системах, а неизвестных
![]() :
: ![]() ,
, ![]()
Недостающие ![]() уравнений дает система уравнений ограничений (2):
уравнений дает система уравнений ограничений (2):
![]() ,
, ![]()
Итак, имеется система из ![]() уравнений для нахождения
уравнений для нахождения ![]() неизвестных:
неизвестных:
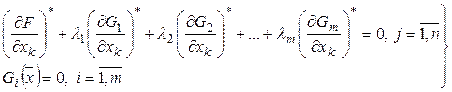 (11)
(11)
Полученный результат – система уравнений (11) составляет основное содержание ММЛ.
Легко понять, что систему уравнений (11) можно получить очень просто, вводя в рассмотрение специально сконструированную функцию Лагранжа (3).
Действительно
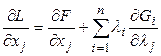 ,
, ![]() (12)
(12)
![]() ,
, ![]() (13)
(13)
Итак, система уравнений (11) представима в виде (используя (12), (13)):
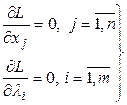 (14)
(14)
Система уравнений (14) представляет необходимое условие в классической задаче условной оптимизации.
Найденное в результате решение этой системы значение вектора ![]() называется условно-стационарной точкой.
называется условно-стационарной точкой.
Для того, чтобы выяснить характер условно-стационарной точки ![]() необходимо воспользоваться достаточными условиями.
необходимо воспользоваться достаточными условиями.
5.3 Достаточные условия в классической задаче условной оптимизации. Алгоритм ММЛ
Эти условия позволяют выяснить, является ли условно-стационарная точка ![]() точкой локального условного минимума, или точкой локального условного максимума.
точкой локального условного минимума, или точкой локального условного максимума.
Относительно просто, подобно тому, как были получены достаточные условия в задаче на безусловный экстремум. Можно получить достаточные условия и в задаче классической условной оптимизации.
Результат этого исследования:
![]()
где ![]() - точка локального условного минимума.
- точка локального условного минимума.
![]()
где ![]() - точка локального условного максимума,
- точка локального условного максимума, ![]() - матрица Гессе с элементами
- матрица Гессе с элементами