Реферат: Классические методы безусловной оптимизации

Вычислим производную:

. (3)

(4)

(5)

Из (3), (4), (5). (6)

Из (5). (5')

Подставим (5') в (3) и получаем:

(6')

Из (6), что множитель Лагранжа характеризует "реакцию" значение (ортогональна значению целевой функции) на изменения параметра .

В общем случае (6) принимает вид:

; (7)

Из (6), (7), что множитель , характеризует изменение при изменении соответствующего -того ресурса на 1.

Если - максимальная прибыль или минимальная стоимость, то , характеризует изменения этой величины при изменении , на 1.

5.6. Классическая задача условной оптимизации, как задача о нахождении седловой точки функции Лагранжа:

Пара называется седловой точкой, если выполняется неравенство.

(1)

Очевидно, что из (1). (2)

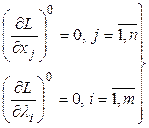Из (2), что . (3)

Как видно система (3) содержит уравнений, подобных тем уравнениям, которые представляют необходимое условие в классической задаче условной оптимизации:

(4)

где - функция Лагранжа.

В связи с аналогией систем уравнений (3) и (4), классическую задачу условной оптимизации можно рассматривать как задачу о нахождении седловой точки функции Лагранжа.