Реферат: Классические методы безусловной оптимизации

Ответ на этот вопрос можно получить, изучив достаточные условия. Эти условия предполагают исследование матрицы вторых производных целевой функции .

2. Достаточные условия для точки локального минимума (максимума)

Представим разложение функции в окрестности точки в ряд Тейлора с точностью до квадратичных по слагаемых.

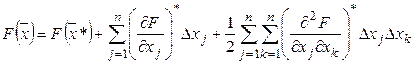(1)

Разложение (1) можно представить более кратко, используя понятие: "скалярное произведение векторов" и "векторно-матричное произведение".

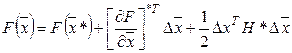(1')

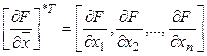
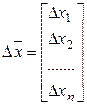
- матрица двух производных от целевой функции по соответствующим переменным.

,

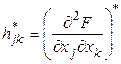Приращение функции на основании (1') можно записать в виде:

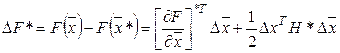(3)

Учитывая необходимые условия:

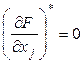, (4)

Подставим (3) в виде:

(4')

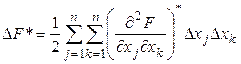(5)

Квадратичная форма называется дифференциальной квадратичной формой (ДКФ).

Если ДКФ положительно определена, то и стационарная точка является точкой локального минимума.

Если же ДКФ и матрица , ее представляющая, отрицательно определены, то и стационарная точка является точкой локального максимума.

Итак, необходимое и достаточное условие для точки локального минимума имеют вид

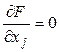
(эти же необходимые условия можно записать так:

, , )

- достаточное условие.

Соответственно, необходимое и достаточное условие локального максимума имеет вид:

, (), .

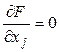Вспомним критерий, позволяющий определить: является ли квадратичная форма и матрица, ее представляющая, положительно определенной, или отрицательно определенной.