Реферат: Классические методы безусловной оптимизации
![]() (5)
(5)
Исследуемая функция ![]() на экстремум можно произвести методом Эйлера – методом безусловной оптимизации непрерывно дифференцируемой функции.
на экстремум можно произвести методом Эйлера – методом безусловной оптимизации непрерывно дифференцируемой функции.
Итак, метод исключения (подстановки) позволяет использовать задачу классической условной оптимизации преобразовать в задачу безусловной оптимизации функции ![]() - функции
- функции![]() переменных при условии (4), позволяющим получить систему выражений (3).
переменных при условии (4), позволяющим получить систему выражений (3).
Недостаток метода исключения: трудности, а иногда и невозможность получения системы выражений (3). Свободный от этого недостатка, но требующий выполнения условия (4) ![]() является ММЛ.
является ММЛ.
5.2. Метод множителей Лагранжа. Необходимые условия в классической задаче условной оптимизации. Функция Лагранжа ![]()
ММЛ позволяет исходную задачу классической условной оптимизации:
![]() (1)
(1)
![]() (2)
(2)
Преобразовать в задачу безусловной оптимизации специально сконструированной функции – функции Лагранжа:
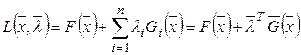 , (3)
, (3)
где ![]() ,
, ![]() - множители Лагранжа;
- множители Лагранжа;
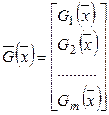 .
.
Как видно, ![]() представляет собой сумму, состоящую из исходной целевой функции
представляет собой сумму, состоящую из исходной целевой функции ![]() и "взвешенной" суммы функций
и "взвешенной" суммы функций ![]() ,
, ![]() - функции, представляющие их ограничения (2) исходной задачи.
- функции, представляющие их ограничения (2) исходной задачи.
Пусть точка ![]() - точка безусловного экстремума функции
- точка безусловного экстремума функции ![]() , тогда, как известно,
, тогда, как известно, 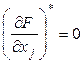 ,
, ![]() , или
, или ![]() (полный дифференциал функции
(полный дифференциал функции ![]() в точке
в точке ![]() ).
).
Используя концепция зависимых и независимых переменных ![]() - зависимые переменные;
- зависимые переменные; ![]() - независимые переменные, тогда представим (5) в развернутом виде:
- независимые переменные, тогда представим (5) в развернутом виде:
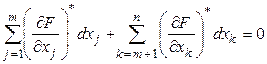 (5')
(5')
Из (2) с очевидностью следует система уравнений вида:
![]() ,
, ![]() (6)
(6)
Результат вычисления полного дифференциала для каждой из функций
![]()
Представим (6) в "развернутом" виде, используя концепцию зависимых и независимых переменных:
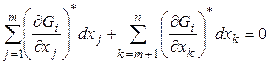 ,
, ![]() (6')
(6')
Заметим, что (6') в отличии от (5') представляет собой систему, состоящую из ![]() уравнений.
уравнений.
Умножим каждое ![]() -ое уравнение системы (6') на соответствующий
-ое уравнение системы (6') на соответствующий ![]() -ый множитель Лагранжа. Сложим их между собой и с уравнением (5') и получим выражение:
-ый множитель Лагранжа. Сложим их между собой и с уравнением (5') и получим выражение:
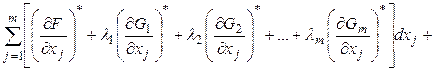
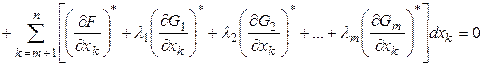 (7)
(7)
Распорядимся множителями Лагранжа ![]() таким образом, чтобы выражение в квадратных скобках под знаком первой суммы (иными словами, коэффициенты при дифференциалах независимых переменных
таким образом, чтобы выражение в квадратных скобках под знаком первой суммы (иными словами, коэффициенты при дифференциалах независимых переменных ![]() ,
, ![]() ) равнялось нулю.
) равнялось нулю.
Термин "распорядимся" множителями Лагранжа вышеуказанным образом означает, что необходимо решить некоторую систему из ![]() уравнений относительно
уравнений относительно ![]() .
.
Структуру такой системы уравнений легко получить приравняв выражение в квадратной скобке под знаком первой суммы нулю: