Реферат: Классические методы безусловной оптимизации

Матрица Гессе имеет размерность .

Размерность матрицы Гессе можно уменьшить, используя условие неравенства нулю якобиана: . При этом условии можно зависимые переменные выразить через независимые переменные , тогда матрица Гессе будет иметь размерность , т.е. необходимо говорить о матрице с элементами

,

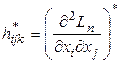тогда достаточные условия будут иметь вид:

, - точка локального условного минимума.

, - точка локального условного максимума.

Доказательство: Алгоритм ММЛ:

1) составляем функцию Лагранжа: ;

2) используя необходимые условия, формируем систему уравнений:

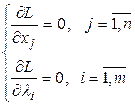
3) из решения этой системы находим точку ;

4) используя достаточные условия, определяем, является ли точка точкой локального условного минимума или максимума, затем находим

1.5.4. Графо-аналитический метод решения классической задачи условной оптимизации в пространстве и его модификации при решении простейших задач ИП и АП

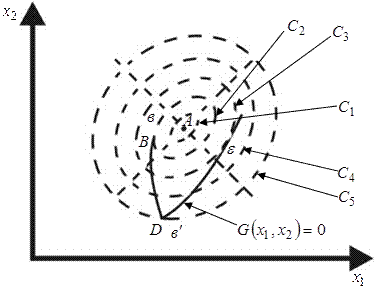
Этот метод использует геометрическую интерпретацию классической задачи условной оптимизации и основан на ряде важных фактов, присущих этой задаче.

; ; ;

В - общая касательная для функции и функции , представляющей ОДР .

Как видно из рисунка точка - точка безусловного минимума, точка точка условного локального минимума, точка - точка условного локального максимума.

Докажем, что в точках условных локальных экстремумов кривая и соответствующие линии уровня

; .

Из курса МА известно, что в точке касания выполняется условие

где - угловой коэффициент касательной, проведенной соответствующей линией уровня; - угловой коэффициент касательной, проведенной к функции

Известно выражение (МА) для этих коэффициентов:

;