Реферат: Лекции по Математике 3

;

2.

Данное уравнение невозможно разрешить относительно производной.

Дифференциальное уравнение может иметь бесконечное множество решений. Чтобы выделить

из этого множества решений какое-то конкретное решение, надо задать дополнительное усло-

вие:

(4)

оно называется начальным условием.

Так как часто в уравнениях независимой переменной является время , поэтому условие (4)

означает, что искомая функция задается в начальный момент времени, отсюда название

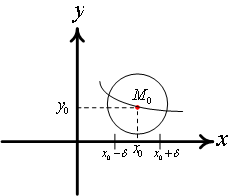
начальное условие. Геометрически начальное условие означает, что задается точка ,

через которую должна проходить искомая интегральная кривая.

Определение 7. Задача нахождения решения уравнения (3), удовлетворяющего условию (4),

называется задачей Коши (или задачей с начальным условием).

1.2 Теорема существования и единственности решения задачи Коши.

Часто бывает трудно решить аналитически дифференциальное уравнение, поэтому большое

значение имеют приближенные методы решения дифференциальных уравнений, которые в

связи с быстрым развитием вычислительной техники приобретают еще большее значение.

Однако, чтобы применять тот или иной метод приближенного интегрирования дифференциаль-

ного уравнения, надо прежде всего быть уверенным в существовании искомого решения, а так-

же и в единственности решения, так как при отсутствии единственности остается неясным, ка-

кое именно решение требуется приближенно определить. Ответ на эти вопросы дает следую-

щая теорема.

Теорема 1(существования и единственности).

Пусть функция в уравнении (3) определена в некоторой области на плоскости .

Если существует окрестность точки , в которой функция :

1) непрерывна по совокупности аргументов;

2) имеет ограниченную частную производную ,

то найдется интервал оси , на котором существует и единственно решение

уравнения (3), удовлетворяющее условию (4).