Реферат: Лекции по Математике 3

вариации произвольной постоянной.

1. Сначала решаем линейное однородное уравнение, соответствующее данному неоднородному

Оно одновременно является и уравнением с разделяющимися переменными, разделим перемен-

ные и проинтегрируем равенство:

, пропотенцируем данное

равенство, получим - это общее решение линейного однородного уравнения.

2. Теперь будем искать общее решение линейного неоднородного уравнения в виде:

, где - неизвестная функция. Тогда

Подставляем функцию и ее производную в уравнение (22), получаем

или .

Теперь разделяем переменные и интегрируем:

Следовательно, общее решение уравнения (22) имеет вид:

.

Пример 12. Найти общее решение уравнения .

Решение. Линейное однородное уравнение, соответствующее данному неоднородному

. Разделяем переменные и интегрируем: ,

потенцируем полученное равенство, получаем .

Будем искать общее решение неоднородного уравнения в виде: . Тогда

. Подставляем все в исходное уравнение, получаем:

. Разделяем переменные и интегрируем

. Подставляем найденную

функцию, получаем общее решение линейного неоднородного уравнения

.

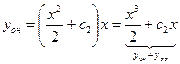Определение 17. Уравнение вида (23),

где называется уравнением Бернулли.

Сначала разделим левую и правую части уравнения (23) на , получим

(24)

Теперь сделаем замену:

(25)

Тогда , подставляем в уравнение (24), получаем:

(26)