Реферат: Лекции по Математике 3

4. Однородное уравнение

,где

- однородные функции оди-

наковой степени однородности

или

4. Замена ,

или

5. Уравнение, приводящееся к однородном или

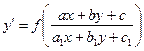
5. а) 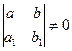, замена ,

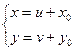где - решение системы

б) 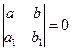, замена

6. Линейное неоднородное уравнение

6. а) решается линейное однородное уравне-

ние : -общее решение;

б) общее решение неоднородного уравне-

ния ищется в виде

7. Уравнение Бернулли , где	7. Делим на , замена , тогда , получаем линейное неодно- родное уравнение
8. Уравнение в полных дифференциалах , где	8. , функция удовлетворяет уравнению

Лекция 3.

1.4 Дифференциальные уравнения высших порядков, допускающие понижение порядка.

Дифференциальное уравнение -ого порядка записывается следующим образом

(30),