Реферат: Лекции по Математике 3

ния уравнения (3), удовлетворяющего условию (4) в достаточно малой окрестности т. .

Геометрически теорема означает, что через т. проходит только одна интегральная

кривая уравнения (3).

Пример 4. Рассмотрим уравнение . Функция определена и непрерывна

на всей плоскости , , 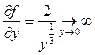следовательно, условие 2 теоремы 1 нарушается в

точках оси . Решениями данного уравнения являются функции , где - констан-

та, и еще . Если искать решение этого уравнения, удовлетворяющее условию , то

таких решений бесконечно много, например, , , 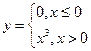и т.д.

Значит через каждую точку оси проходят по крайней мере две интегральные кривые, следо-

вательно, в точках оси нарушается единственность.

Определение 8. Общим решением дифференциального уравнения (3) в некоторой области

существования и единственности решения задачи Коши называется однопараметрическое се-

мейство функций , зависящих от одной независимой переменной и одной произ-

вольной постоянной (называемой параметром), такое, что

1) при любом допустимом значение параметра функция этого семейства является решением

уравнения (3);

2) каково бы ни было начальное условие (4), можно подобрать такое значение параметра , что решение будет удовлетворять данному условию.

При этом предполагается, что т. принадлежит области существования и единственности

решения задачи Коши.

Определение 9. Частным решением уравнения (3) называется решение, получаемое из общего

при каком-либо конкретном значении параметра.

Определение 10. Уравнение (5),

неявно задающее решение уравнения (3), называется общим интегралом.

Определение 11. Уравнение (6),

где - конкретное значение параметра , называется частным интегралом.

Определение 12. Решение уравнения (3) называется особым, если в каждой его точке

нарушается единственность, то есть через каждую его точку кроме данного решения проходит и другое решение уравнения (3), не совпадающее с в сколь угодно малой окрестности точки .

1.3 Уравнения первого порядка.

Дифференциальное уравнение называется интегрируемым в квадратурах, если его общее реше-