Реферат: Лекции по Математике 3

Определение 15. Уравнение (16),

где - константы, причем называется уравнением, приводящимся к

однородному.

В случае, когда , уравнение (16) будет являться однородным.

Рассмотрим следующие случаи:

1.

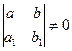
Введем новые переменные и следующим образом:

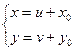(17),

где пока неопределенные константы, , тогда уравнение (16) примет вид

Если подобрать таким образом, чтобы

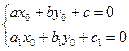(18),

то есть являются решением системы (18), тогда получим однородное уравнение:

(19)

Найдем его общий интеграл, а затем вернемся к старым переменным и получим общий ин-

теграл уравнения (16).

2. 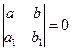, это означает, что строки определителя пропорциональны, то есть

, значит уравнение (16) имеет вид:

(20)

Это уравнение приводится к уравнению с разделяющимися переменными заменой

.

Аналогично интегрируется уравнение

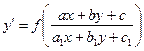(21),

где - заданная непрерывная функция.

Пример 10. Найти общий интеграл уравнения .

Решение. Так как , для приведения данного уравнения к однородному

надо сделать замену, для этого сначала решим систему:

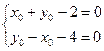, получим .

Тогда сделаем следующую замену , подставляем в исходное уравнение, получаем

или - это однородное уравнение, для его решения сделаем

замену или , , подставляем в однородное уравнение, получа-

ем или .

Преобразуем полученное уравнение, чтобы можно было разделить переменные:

, тогда