Реферат: Поиски более рационального способа решения систем линейных уравнений с двумя переменными - методом подстановки
![]()
Подставляя это значение у в первое из системы уравнений (1), автор приходит к квадратному уравнению:
![]()
Решая это уравнение по правилу, применяемому нами в настоящее время, автор находит х, после чего определяет у. Итак, хотя вавилоняне и не имели алгебраической символики, они решали задачи алгебраическим методом.
Диофант, который не имел обозначений для многих неизвестных, прилагал немало усилий для выбора неизвестного таким образом, чтобы свести решение системы к решению одного уравнения. Вот один пример из его “Арифметики".
Задача 2. “Найти два числа, зная, что их сумма равна 20, а сумма их квадратов - 208".
Эту задачу мы решили бы путем составления системы уравнений:
![]()
Диофант же, выбирая в качестве неизвестного половину разности искомых чисел, получает (в современных обозначениях):
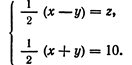
Складывая эти уравнения, а затем вычитая одно из другого (все это Диофант производит устно), получаем
x = 2 + 10; у = 10 - 2. Далее, х2 + у2 = (г + lO) 2 + (10 - г) 2 == 2 z2 + 200 .
Таким образом,
2 z2 + 200 = 208,
Откуда
z = 2; х = 2 + 10 = 12; у = 10 - 2 = 8.
В поисках различных решений я обнаружил следующее.
Основные методы решения рациональных уравнений.
1) Простейшие: решаются путём обычных упрощений - приведение к общему знаменателю, приведение подобных членов и так далее. Квадратные уравнения ax2 + bx + c = 0 решаются по выведенной нами формуле
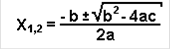
Также используется теорема Виета:
x1 + x2 = - b / a; x1 x2 = c / a.
2) Группировка: путём группировки слагаемых, применения формул сокращённого умножения привести (если удастся) уравнение к виду, когда слева записано произведение нескольких сомножителей, а справа - ноль. Затем приравниваем к нулю каждый из сомножителей.
3) Подстановка: ищем в уравнении некоторое повторяющееся выражение, которое обозначим новой переменной, тем самым упрощая вид уравнения. В некоторых случаях очевидно что удобно обозначить. Например, уравнение (x2 + x- 5) / x + 3x / (x2 + x- 5) + 4 = 0,легко решается с помощью подстановки (x2 + x- 5) / x = t, получаем t + (3/t) + 4 = 0. Или: 21/ (x2 - 4x+ 10) - x2 + 4x = 6. Здесь можно сделать подстановку x2 - 4 = t. Тогда 21/ (t + 10) - t = 6 и т.д.
В более сложных случаях подстановка видна лишь после нескольких преобразований. Например, дано уравнение
(x2 + 2x) 2 - (x +1) 2 = 55.
Переписав его иначе, а именно (x2 + 2x) 2 - (x2 + 2x + 1) = 55, сразу увидим подстановку x2 + 2x=t.
Имеем t2 - t- 56 = 0, t1 = - 7, t2 = 8. Осталось решить x2 + 2x = - 7 и x2 + 2x = 8. В ряде других случаев удобную подстановку желательно знать “заранее". Например
1) Уравнение (x + a) 4 + (x + b) 4 = cсводится к биквадратному, если сделать подстановку