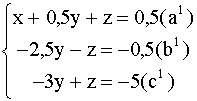Реферат: Поиски более рационального способа решения систем линейных уравнений с двумя переменными - методом подстановки
2) Симметрическое уравнение (возвратное) a0 xn + a1 xn - 1 + … + a1 x + a0 = 0 (коэффициенты членов, равностоящих от концов, равны) решается с помощью подстановки x + 1/x = t, если n - чётное; если n - нечётное, то уравнение имеет корень x = - 1.
3) Уравнение вида (x + a) (x + b) (x + c) (x + d) = l сводится к квадратному, если a + b = c + dи т.д.
4) Подбор: при решении уравнений высших степеней рациональные корни уравнения an xn + an - 1 xn - 1 + …+ a1 x + a0 = 0 ищем в виде p / q, где p - делитель a0 , q - делитель an , p и qвзаимно просты, pÎZ, qÎN.
5) “Искусство”, т.е. решать пример нестандартно, придумать “свой метод", догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и умножить и т.д.
6) Уравнения с модулем: при решении уравнений с модулем используется определение модуля и метод интервалов. Напомним, что
f (x), если f (x) ³0,|f (x) | =
f (x), если f (x) < 0.
Это уже изученные методы и широко применяемые в практической математике. Выделенные жирным курсивом - это методы мною изучаемые 5) “Искусство", - это то, что мне предстоит найти.
Хотелось бы остановится на некоторых из них.
Метод Гаусса.
Пусть дана система линейных уравнений
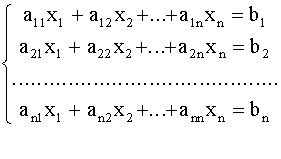(1)
Коэффициенты a 11, 12, ..., a 1n, ..., a n1, b 2, ..., b n считаются заданными. Вектор - строка í x 1, x 2, ..., x n ý - называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство.
Определитель n-го порядка D = ç A ê = ç a ij ç, составленный из коэффициентов при неизвестных, называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи.
a). Если D ¹ 0, то система (1) имеет единственное решение, которое может быть найдено методом ГАУССА. б). Если D = 0, то система (1) либо имеет бесконечное множество решений, либо несовместна, т.е. решений нет.
1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.
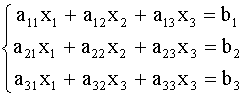(2).
Метод Гаусса решения системы (2) состоит в следующем: Разделим все члены первого уравнения на 
, а затем, умножив полученное уравнение на 
, вычтем его соответственно из второго и третьего уравнений системы (2). Тогда из второго и третьего уравнений неизвестное 
будет исключено, и получиться система вида:
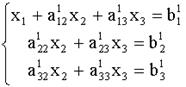(3)
Теперь разделим второе уравнение системы (3) на 
, умножим полученное уравнение на 
и вычтем из третьего уравнения. Тогда из третьего уравнения неизвестное 
будет исключено и получиться система треугольного вида:
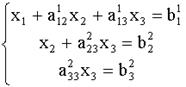(4)
Из последнего уравнения системы (4) находим 
, подставляя найденное
подставляя найденное значение в первое уравнение, находим .
Методом Гаусса решить систему:
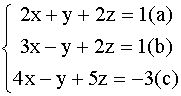
Решение: Разделив уравнение (а) на 2, получим систему
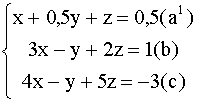
Вычтем из уравнения (b) уравнение 
, умноженное на 3, а из уравнения (c) - уравнение , умноженное на 4.
