Реферат: Поиски более рационального способа решения систем линейных уравнений с двумя переменными - методом подстановки

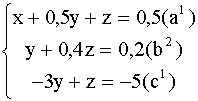
Вычтем из уравнения () уравнение , умноженное на - 3:

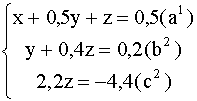
Из уравнения находим Z=-2; подставив это значение в уравнение , получим Y=0,2-0,4Z=0,2-0,4 (-2) =1; наконец, подставив значение Z=-2 и Y=1 в уравнение (a ¹⁾ , находим X=0,5-0,5Y-Z=0,5-0,5 1 - (-2) =2. Итак, получаем ответ X=2, Y=1, Z=-2.

Проверка:

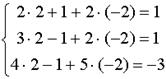
Линейные уравнения.

Уравнения вида ax+b=0, где a и b - некоторые постоянные, называется линейным уравнением.

Если a¹0, то линейное уравнение имеет единственный корень: x = - b /a.

Если a=0; b¹0, то линейное уравнение решений не имеет.

Если a=0; b=0, то, переписав исходное уравнение в виде ax = - b, легко видеть, что любое xявляется решением линейного уравнения.

Уравнение прямой имеет вид: y = ax + b.

Если прямая проходит через точку с координатами X₀ и Y₀ , то эти координаты удовлетворяют уравнению прямой, т.е. Y₀ = aX₀ + b.

Пример 1.1 Решить уравнение

2x- 3 + 4 (x- 1) = 5.

Решение. Последовательно раскроем скобки, приведём подобные члены и найдём x: 2x- 3 + 4x- 4 = 5, 2x + 4x = 5 + 4 + 3,6x = 12, x = 2.

Ответ: 2.

Пример 1.2 Решить уравнение 2x - 3 + 2 (x- 1) = 4 (x- 1) - 7.

Решение.2x + 2x- 4x = 3 +2 - 4 - 7, 0x = - 6.

Ответ: Æ.

Пример 1.3 Решить уравнение.

2x + 3 - 6 (x- 1) = 4 (x- 1) + 5.

Решение.

2x- 6x + 3 + 6 = 4 - 4x + 5,- 4x + 9 = 9 - 4x,

4x + 4x = 9 - 9,0x = 0.

Ответ: Любое число.

Системы линейных уравнений.

Уравнение вида

a₁ x₁ + a₂ x₂ + … + a_n x_n = b,