Реферат: Поле комплексных чисел

Из формул Эйлера следует, что для

.

Складывая и вычитая эти равенства находим, что для :

(1) ;

(2) .

Как известно, из курса математического анализа, гиперболические косинус, синус, тангенс, котангенс, соответственно, , для , определяются равенствами:

; ;

; .

Если в формулах (1), (2), заменить на , то мы получим формулы для определения значений . Эти формулы выражают гиперболические формулы через тригонометрические. Для :

; ;

; .

п.9. Корни из комплексных чисел.

Определение. Пусть , . Комплексное число называется корнем степени из , если .

Теорема 6. Пусть , - множество всех корней степени из 1. Тогда алгебра - группа, (которая называется группой корней степени из 1).

Доказательство. Пусть .

Проверим, что умножение – бинарная операция. Имеем - корень степени из 1.

Проверим, что - унарная операция. Имеем - корень степени из 1.

Очевидно, что 1 – корень степени из 1.

Доказано, что - алгебра.

То, что алгебра - группа, следует из свойств комплексных чисел.

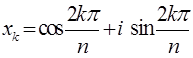Теорема 7. Для существует точно различных корней степени из 1, , . (1)

Все корни расположены в вершинах правильного n-угольника, вписанного в окружность единичного радиуса, одна из которых расположена в точке с координатами (1, 0).

Доказательство. Проверим сначала, что числа , заданные равенством (1), являются корнями степени из 1. Действительно, .

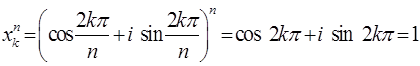Докажем, что любой корень степени из 1 может быть вычислен по формуле (1). Т.к. , то можно записать в показательой форме .

Имеем . Поэтому , , , где . По теореме о делении с остатком, существуют такие , что , где .

Значит, , , 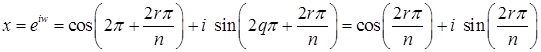т.е. вычисляется по формуле (1).

Изобразив числа, заданные формулой (1), на комплексной плоскости, мы увидим, что они расположены в вершинах правильного n-угольника, вписанного в окружность единичного радиуса, одна из которых расположена в точке с координатами (1, 0). В частности, числа, заданные формулой (1), попарно различны.

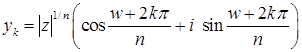Теорема 8. Пусть , , , . Тогда существует точно различных корней степени из , , . (2)

Доказательство. Проверим сначала, что числа , заданные равенством (2), являются корнями степени из . Действительно, .