Реферат: Поле комплексных чисел

- bi `a

Пример. Изобразим на комплексной плоскости, на Рис.2, множества, заданные, соответственно, следующими условиями: ; ; .

y | z | =1 y | z |£1 y | z |³1

i i i

- 1 1 - 1 1 - 1 1

0 0 0

- i - i - i

Рис.2.

Пусть записано в алгебраической форме . Имеем

.

Из Рис.3 видно, что геометрический смысл модуля разности комплексных чисел - расстояние между этими числами.

y

b a

d |b-d|

b|a-c|

Рис.3.

0 c a x

Пример. Изобразим на комплексной плоскости, на Рис.4, множества, заданные, соответственно, следующими условиями: ; .

y y

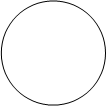
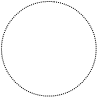
| z-1| =2 0

x

- i

- 1 0 1 3 x |z+i |> 1

- 2i

Рис.4.

Геометрическая интерпретация комплексных чисел векторами плоскости

Поставим в соответствие числу связаный вектор плоскости с началом в начале координат и с концом в точке . Установленное соответствие является биекцией между множеством комплексных чисел и множеством связаных векторов плоскости с началом в начале координат. Проиллюстрируем эту связь на Рис.5.