Реферат: Решение задачи об оптимальной интерполяции с помощью дискретного преобразования Фурье (ДПФ)

3.

4.Если а ≠ 0, то скалярный квадрат вектора а строго положителен, т.е.

(а. а) > 0, а если (а, а) = 0, то а = 0.

Комплексное линейное пространство называется унитарным пространством, если в нём задано скалярное умножение.

Векторы а и b называются ортогональными, если их скалярное произведение равно нулю

(а, b) = 0.

Система векторов называется ортогональной системой, если все векторы этой системы попарно ортогональны.

Назовём вектор b нормированным, если его скалярный квадрат равен единице

(b, b) = 1.

При этом, если - ортонормированная база и векторы а, b

имеют в этом базе записи

а = , , 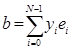то .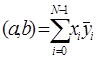

Также имеем равенство

(3)

3.Вычеты. Пусть и – натуральное число. Существует единственное целое число , такое, что

(4)

Оно называется целой частью дроби и обозначается

Разность называется вычетом по модулю и обозначается .

4

Нетрудно показать, что

. (5)

Действительно, умножим неравенства (4) на и вычтем .

Получим , что равносильно (5).

4.Функции комплексного переменного. На плоскостях комплексных переменных z и w рассмотрим соответственно множества и .

Если указан закон f, по котором каждому значению сопоставляется единственное значение , то говорят, что на множестве Е определена однозначная функция комплексного переменного z и пишут w=f(z).

Функции определяются как суммы степенных рядов:

, , . (6)

Из этих равенств непосредственно можно получить следующие формулы Эйлера:

, , . (7)