Реферат: Решение задачи об оптимальной интерполяции с помощью дискретного преобразования Фурье (ДПФ)

На самом деле,

при

–периодическим является и Поэтому достаточно проверить равенство (1) при .

При оно тривиально. Пусть Из формулы для суммы членов геометрической прогрессии имеем

при

Положив , получим

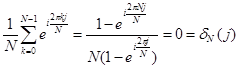при .

Равенство доказано.

1.Непрерывное преобразование Фурье и формула обращения.

Функция , заданная на всей числовой прямой и определяемая формулой

, (2)

называется преобразованием Фурье исходной функции .

13

Формула, выражающая через её преобразование Фурье и имеющая вид

, (3)

называется формулой обращения для непрерывного преобразования Фурье.

Следует обратить внимание на сходство между формулами (1) и (2).

Вторая из них отличается от первой лишь знаком в показателе и множителем перед интегралом.

2.Дискретное преобразование Фурье (ДПФ). Определение.

ДПФ – это отображение

,

сопоставляющее вектору вектор со значениями

(4)

Вектор X называется спектром Фурье вектора x или просто спектром, а величины X(k) – компонентами спектра или спектральными составляющими соответствующего вектора.

Теорема 1. Имеет место формула обращения

(5)

Доказательство. Из формул (1), (4) и из формулы (1) предыдущего параграфа имеем

Теорема доказана.