Реферат: Решение задачи об оптимальной интерполяции с помощью дискретного преобразования Фурье (ДПФ)

Ставится задача следующим образом. Пусть где и

Также считается известными и

Требуется узнать, можно ли найти при условии, что

В приводимой ниже теореме показывается, что при некотором предположении координаты вектора полностью восстанавливаются.

Теорема. Если спектр вектора равен нулю на некотором множестве , то

(1)

Доказательство. По формуле обращения для ДПФ, учитывая условию теоремы, приходим к следующему равенству

(2)

Зафиксируем и пусть Продолжив периодически с периодом на , получим вектор , принадлежащий Вычислим его ДПФ:

Применяя формулу обращения, приходим к равенству

20

Подставив это выражение в (2), придём к (1). Действительно,

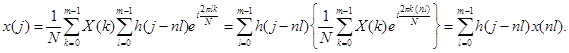
Теорема доказана.

Упростим формулу для h. Очевидно, что

Так как

.

Аналогичным образом получаем

.

При имеем

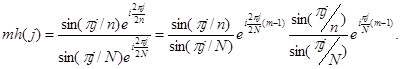
Итак, получаем

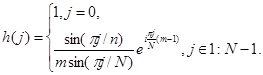(3)

21

В простейшем случае, когда формула (3) принимает вид