Реферат: Решение задачи об оптимальной интерполяции с помощью дискретного преобразования Фурье (ДПФ)

Проверим это. При всех имеем

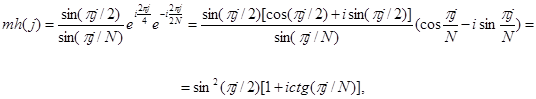
что равносильно требуемому.

В случае нашу теорему можно переформулировать так: если на основном периоде половина значений спектра с индексами равна нулю, то вектор восстанавливается по половине своих

компонентов с помощью формулы

где h имеет вид (4).

22

§5.Интерполяционная задача.

Рассмотрим следующую интерполяционную задачу

(1)

В этой задаче требуется построить вектор , который в узлах принимает заданные значения . Также известно, что старшие коэффициенты Фурье равны нулю.

Решение данной интерполяционной задачи сформулируем в виде теоремы.

Теорема. Решением задачи (1) является вектор

(2)

Доказательство. Однородная система

согласно формуле (1) из предыдущего параграфа имеет только нулевое решение. Таким образом, задача (1) однозначно разрешима при любых комплексных Рассмотрим решение этой задачи. Аргумент представим в виде В силу определения и формулы (1) предыдущего параграфа, получим

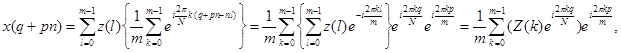
Теорема доказана.

23

§ 6. Свёртка векторов

Свёрткой векторов называется вектор с компонентами

(1)

Теорема 1 (о свёртке). Пусть Тогда

(2)

где справа стоит покомпонентное произведение спектров§, которое определяется следующим образом

Доказательство.